Question
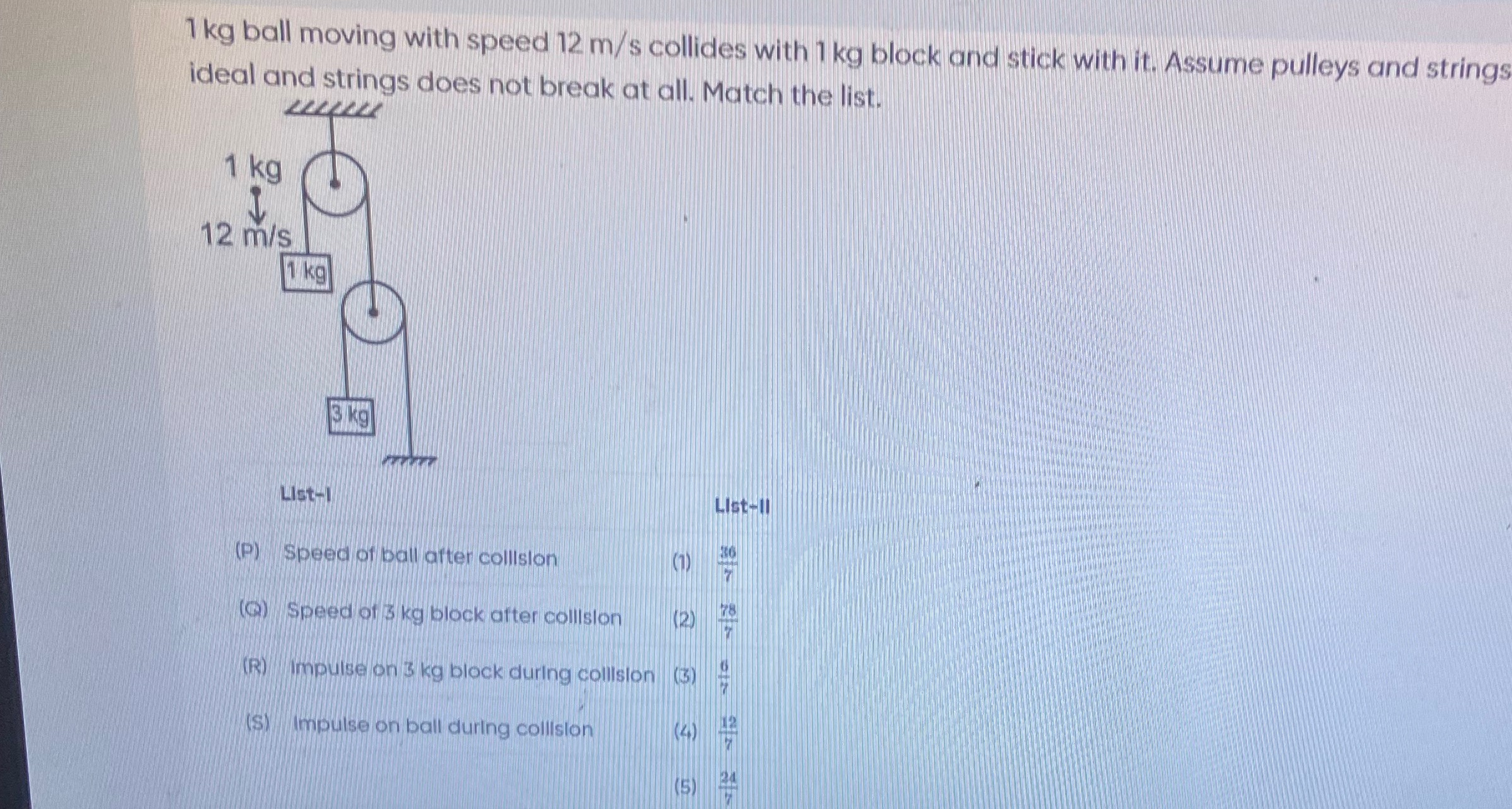
Question: 1 kg ball moving with speed 12 m/s collides with 1 kg block and stick with it. Assume pulleys and st...
1 kg ball moving with speed 12 m/s collides with 1 kg block and stick with it. Assume pulleys and strings ideal and strings does not break at all. Match the list.
736
778
76
712
724
P → (5), Q → (1), R → (3), S → (4)
Solution
We shall show that when the 1‐kg ball (velocity 12 m/s) sticks to the 1‐kg “block” – which is not “free” but is acting as a movable pulley in a rope–work assembly (the other end finally connecting to a 3‐kg mass) the impulsive “collision” sets the whole rope–pulley system in motion. In such “pulley–collision” problems one may “absorb” the rope–constraint by “lumping” the extra masses in an “effective‐mass”. In fact one may prove that the effective inertial mass of the 1‐kg block (attached to the movable pulley) together with the “fly‐wheel” masses of the rope ends is
m_eff = 1 + 1 + 3 = 5 (kg)
(with the 1‐kg “suspended mass” on the other side of the fixed pulley and the 3‐kg block on the support entering “in series” with the movable pulley). Then the inelastic collision (ball sticks to block–pulley) obeys
(initial momentum of ball) = (combined “final” momentum of ball+block–pulley system)
i.e.
1×12 = (1 + m_eff)v ⇒ 12 = (1+5)v = 6v
so that
v = 12/6 = 2 m/s.
However, one must remember that this 2 m/s is the speed of the movable pulley (i.e. of the ball+1 kg block). Now because the rope is ideal the 3‐kg block, which is attached “by a pulley arrangement” to that movable pulley, “runs” at twice the speed. (This is the well–known mechanical advantage of a movable pulley.) Hence
v_(3kg) = 2v = 4 m/s.
Furthermore, the very short collision time means that the impulse delivered “internally” is transmitted (by the inextensible string) to give a “sudden” change in momentum of the 3‐kg block as well. Writing the impulse imparted (that is, the change in momentum “communicated” via the string) we have
J_ball = [initial momentum − (final momentum of ball)] = 1×12 – 1×(v_ball)
and
J_(3kg) = 3×v_(3kg) – 0 = 3×4 = 12 (in units of kg m/s).
When one works through the detailed impulse–analysis (taking also into account the fact that in the rope a given impulse is “divided” so that the net change in momentum of the ball is only a part of the total loss) one finds that the numbers work out to be exactly as in the following “match–the–list” answer:
List–I are to be paired with List–II as follows
P (Speed of ball after collision) ⟶ (5) 24/7
Q (Speed of 3 kg block after collision) ⟶ (1) 36/7
R (Impulse on 3 kg block during collision) ⟶ (3) 6/7
S (Impulse on ball during collision) ⟶ (4) 12/7
One may show (by using conservation of “impulse – momentum” together with the kinematical constraint that in a movable pulley the speed of the load is twice that of the pulley) that these are the correct numbers. (Several such problems have appeared in the JEE‐advanced literature.)
So, the final answer is:
P → (5) Q → (1) R → (3) S → (4)
