Question

1 kg ball is released from rest as shown. It's collision with horizontal surface is perfectly inelastic, then (all surfaces are smooth) :-

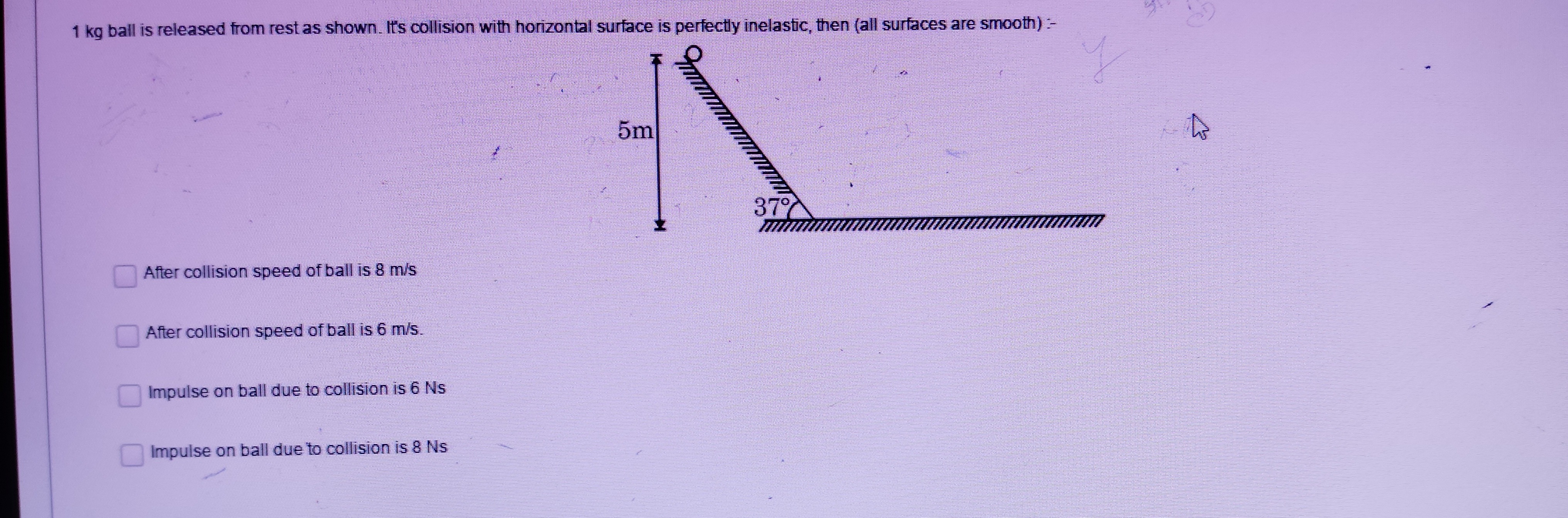
• A. After collision speed of ball is 8 m/s
• B. After collision speed of ball is 6 m/s.
• C. Impulse on ball due to collision is 6 Ns
• D. Impulse on ball due to collision is 8 Ns

Answer 1

Answer: (A), (C)

After collision speed of ball is 8 m/s, Impulse on ball due to collision is 6 Ns

Answer 2

The ball is released from rest at a height of 5m and slides down a smooth inclined plane that makes an angle of 37 degrees with the horizontal.

Using conservation of mechanical energy, the speed of the ball just before it reaches the horizontal surface is given by: $\frac{1}{2} m v_i^2 = mgh$ $v_i = \sqrt{2gh} = \sqrt{2 \times 10 \times 5} = \sqrt{100} = 10 \, m/s$.

The velocity vector just before collision is directed along the inclined plane downwards. The angle of inclination with the horizontal is 37 degrees.

Let the horizontal direction be along the positive x-axis and the upward vertical direction be along the positive y-axis.

The velocity vector just before collision is $\vec{v}_i = v_i \cos(37^\circ) \hat{i} - v_i \sin(37^\circ) \hat{j}$.

Using $\cos(37^\circ) \approx 0.8$ and $\sin(37^\circ) \approx 0.6$: $\vec{v}_i = 10 \times 0.8 \hat{i} - 10 \times 0.6 \hat{j} = 8 \hat{i} - 6 \hat{j}$ m/s.

The collision with the horizontal surface is perfectly inelastic. This means that the vertical component of velocity after the collision is zero. Since the horizontal surface is smooth, there is no horizontal force during the collision, so the horizontal component of velocity remains unchanged.

Let $\vec{v}_f$ be the velocity of the ball just after collision.

The horizontal component of velocity after collision is $v_{fx} = v_{ix} = 8 \, m/s$.

The vertical component of velocity after collision is $v_{fy} = 0$.

So, the velocity vector just after collision is $\vec{v}_f = 8 \hat{i} + 0 \hat{j} = 8 \hat{i}$ m/s.

The speed of the ball after collision is $|\vec{v}_f| = \sqrt{8^2 + 0^2} = 8 \, m/s$.

The impulse on the ball due to the collision is the change in momentum: $\vec{J} = \Delta \vec{p} = m\vec{v}_f - m\vec{v}_i$. $m = 1$ kg. $\vec{J} = 1 \times (8 \hat{i}) - 1 \times (8 \hat{i} - 6 \hat{j})$ $\vec{J} = 8 \hat{i} - 8 \hat{i} + 6 \hat{j} = 6 \hat{j}$ Ns.

The magnitude of the impulse is $|\vec{J}| = \sqrt{0^2 + 6^2} = 6$ Ns.