Question

(1) Is $(A \cup B) \cup C = A \cup (B \cup C)?$
(2) Is $(A \cap B) \cap C = A \cap (B \cap C)?$

Answer 1

In this question, we are asked to prove the commutative property of the unions and the intersections of sets. Begin by assuming set A, B and C. Then find out the LHS of the given equation first and then the RHS step by step. If LHS = RHS, then the given statements are correct, otherwise not.

Complete step-by-step answer:
(1) In this question, we have to prove that $(A \cup B) \cup C = A \cup (B \cup C)$.
We will prove it by assuming certain sets.
Let $A = \\{ 1,2,3\\}$,$B = \\{ 4,5,6\\}$and $C = \\{ 7,8,9\\}$.
Let us start with LHS first.
LHS = $(A \cup B) \cup C$
We will find $(A \cup B)$ and using it, we will find $(A \cup B) \cup C$. $(A \cup B)$ includes all the elements in A and B.
$\Rightarrow (A \cup B) = \\{ 1,2,3,4,5,6\\}$
Now let us find $(A \cup B) \cup C$ using $(A \cup B)$ and set C. $(A \cup B) \cup C$ includes all the elements in $(A \cup B)$and C.
$\Rightarrow (A \cup B) \cup C = \\{ 1,2,3,4,5,6,7,8,9\\}$ …..…. (1)
Next, we will find the RHS of the given equation, beginning with finding $(B \cup C)$. It will include all the elements in B and C.
$\Rightarrow (B \cup C) = \\{ 4,5,6,7,8,9\\}$
Now let us find $A \cup (B \cup C)$ using $(B \cup C)$. $A \cup (B \cup C)$ will include all the elements in $(B \cup C)$ and A.
$\Rightarrow A \cup (B \cup C) = \\{ 1,2,3,4,5,6,7,8,9\\}$....…. (2)
From (1) and (2), we can infer that LHS = RHS.
Hence, $(A \cup B) \cup C = A \cup (B \cup C)$.
(2) In this part, we have to prove that $(A \cap B) \cap C = A \cap (B \cap C)$.
Using the same approach as in the above question, let us assume some sets.
Let $A = \\{ 1,2,3,4\\}$, $B = \\{ 2,3,4,5\\}$ and $C = \\{ 3,4,5,6\\}$.
Let us start with LHS first.
LHS =$(A \cap B) \cap C$
We will find $(A \cap B)$ first and using it we will find $(A \cap B) \cap C$. $(A \cap B)$ will include only those elements which are common in A and B.
$\Rightarrow (A \cap B) = \\{ 2,3,4\\}$
Next, we will find $(A \cap B) \cap C$ using $(A \cap B)$. It will include the common elements of $(A \cap B)$ and C.
$\Rightarrow (A \cap B) \cap C = \\{ 3,4\\}$ …..…. (3)
Now we will find the RHS of the given equation. Let us find $(B \cap C)$. $(B \cap C)$ will include only those elements which are common in B and C.
$\Rightarrow (B \cap C) = \\{ 3,4,5\\}$
Using this we will find $A \cap (B \cap C)$. It will include the common elements of $(B \cap C)$ and A.
$\Rightarrow A \cap (B \cap C) = \\{ 3,4\\}$ …..…. (4)
From (3) and (4), we can infer that LHS = RHS.
Hence, $(A \cap B) \cap C = A \cap (B \cap C)$.

Note: This question can also be solved using Venn diagrams.
(1) We have to prove that $(A \cup B) \cup C = A \cup (B \cup C)$. On the LHS, we will mark the $(A \cup B)$ using yellow colour and on RHS, we will mark $(B \cup C)$ using yellow colour. Then we will mark the area covered by $(A \cup B) \cup C$ and $A \cup (B \cup C)$ using blue colour on both the sides, (when blue is mixed with yellow, it gives green).

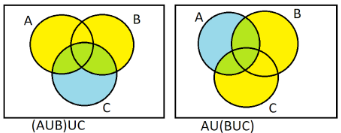
As a result, we can see that the entire figure is covered using colours. The space covered on the LHS figure and on the RHS figure is the same. Therefore, LHS=RHS.
(2) We have to prove that $(A \cap B) \cap C = A \cap (B \cap C)$. On the LHS, we will mark the $(A \cap B)$ with yellow colour and on RHS, we will mark $(B \cap C)$ with yellow colour.

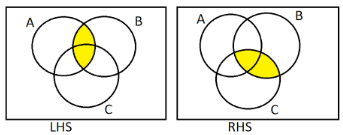
Then we will mark the area covered by $(A \cap B) \cap C$ and $A \cap (B \cap C)$ using green colour on both sides.

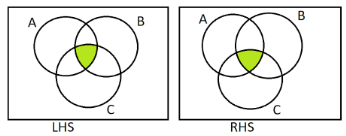
As a result, we can see that the common part (green coloured area) on both sides is the same. Hence, $(A \cap B) \cap C = A \cap (B \cap C)$.