Question

In which part slope of graph is continuously increasing -

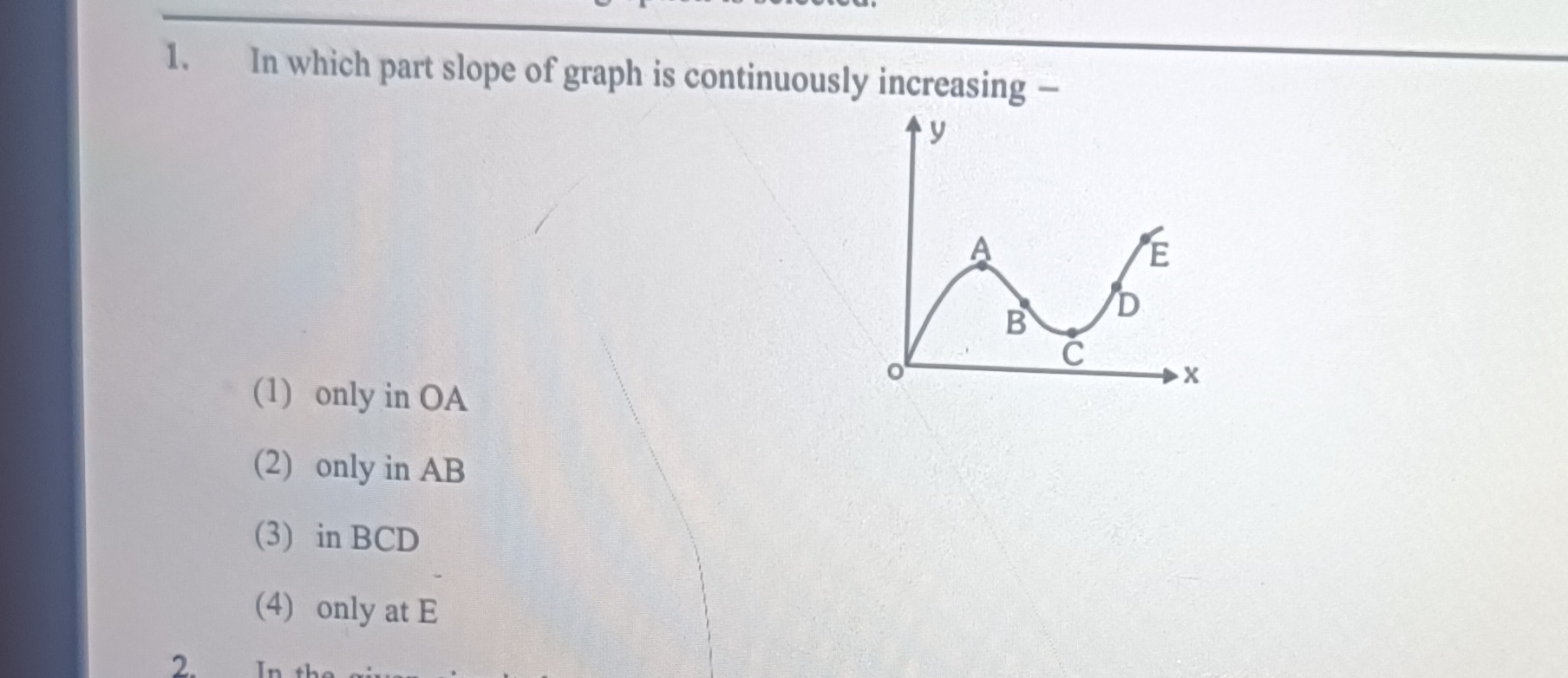
• A. only in OA
• B. only in AB
• C. in BCD
• D. only at E

Answer 1

Answer: (C)

3

Answer 2

To determine where the slope of the graph is continuously increasing, we need to analyze the concavity of the curve or visualize the tangent lines.

The slope of a graph is increasing when the curve is concave up (bowed upwards). Conversely, the slope is decreasing when the curve is concave down (bowed downwards).

Let's examine each segment:

1. Segment OA: The curve is concave down. The slope starts positive and decreases, becoming zero at point A (a local maximum). So, the slope is decreasing in OA.
2. Segment AB: The curve is still concave down. The slope is negative and becomes more negative as we move from A to B. So, the slope is decreasing in AB.
3. Segment BC: The curve is concave up. The slope is negative at B, then increases, becoming zero at point C (a local minimum). So, the slope is increasing in BC.
4. Segment CD: The curve is concave up. The slope is zero at C, then increases, becoming positive and steeper as we move towards D. So, the slope is increasing in CD.
5. Segment DE: The curve becomes concave down again. The slope is positive at D, but then it starts to flatten out, meaning the positive slope is decreasing as we move towards E. So, the slope is decreasing in DE.

Combining the observations for BC and CD, we see that the curve is concave up throughout the entire segment from B to D. This means the slope is continuously increasing in the region BCD.

• From B to C, the slope changes from a negative value to zero (increasing).
• From C to D, the slope changes from zero to a positive value (increasing).

Therefore, the slope of the graph is continuously increasing in the part BCD.