Question

In the given figure linear acceleration of solid cylinder of mass m₂ is a₂. Then angular acceleration $\alpha_2$ is (given that there is no slipping).

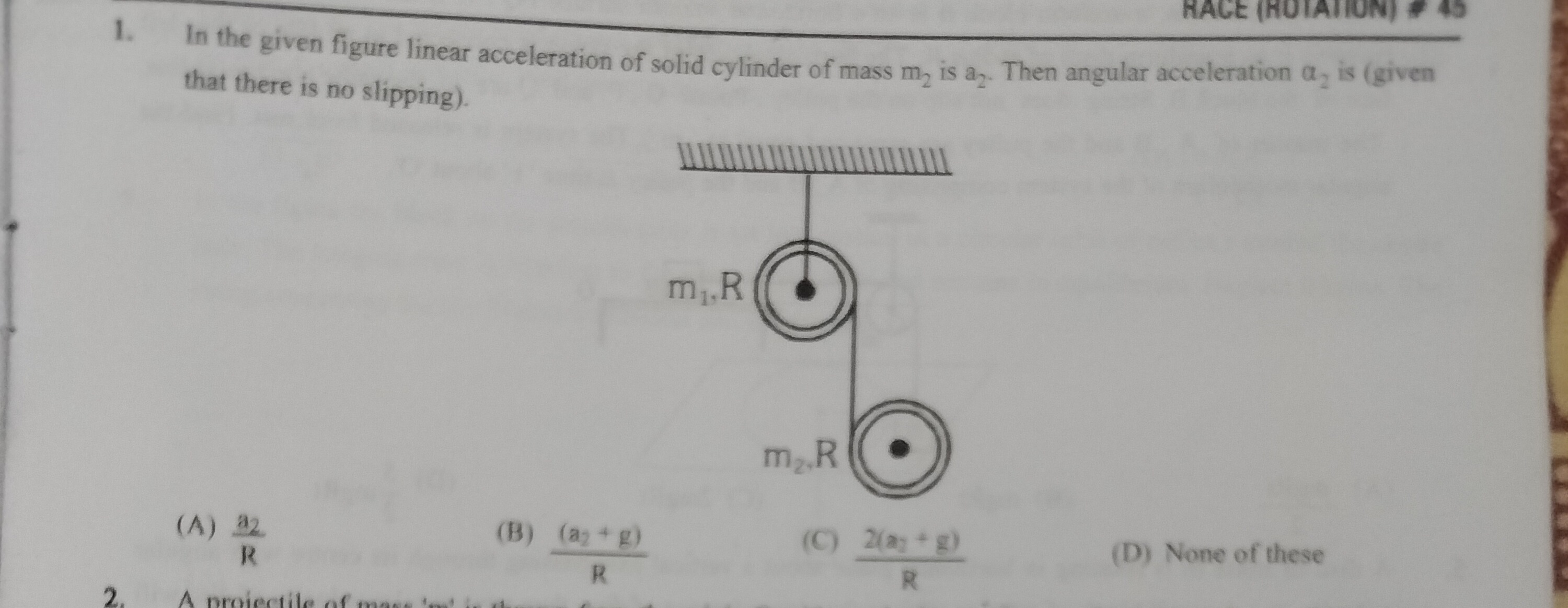
• A. $\frac{a_2}{R}$
• B. $\frac{(a_2 + g)}{R}$
• C. $\frac{2(a_1 + g)}{R}$
• D. None of these

Answer 1

Answer: (A)

$\frac{a_2}{R}$

Answer 2

For a cylinder undergoing pure rolling (no slipping), the linear acceleration of its center of mass ($a_2$) is directly proportional to its angular acceleration ($\alpha_2$) and the radius ($R$). The relationship is given by the kinematic equation for rolling without slipping: $a_2 = R\alpha_2$. Rearranging this equation to solve for $\alpha_2$, we get $\alpha_2 = \frac{a_2}{R}$. This equation holds true regardless of the mass of the cylinder ($m_2$), the acceleration due to gravity ($g$), or the presence of other components in the system, as long as the no-slipping condition is met.