Question

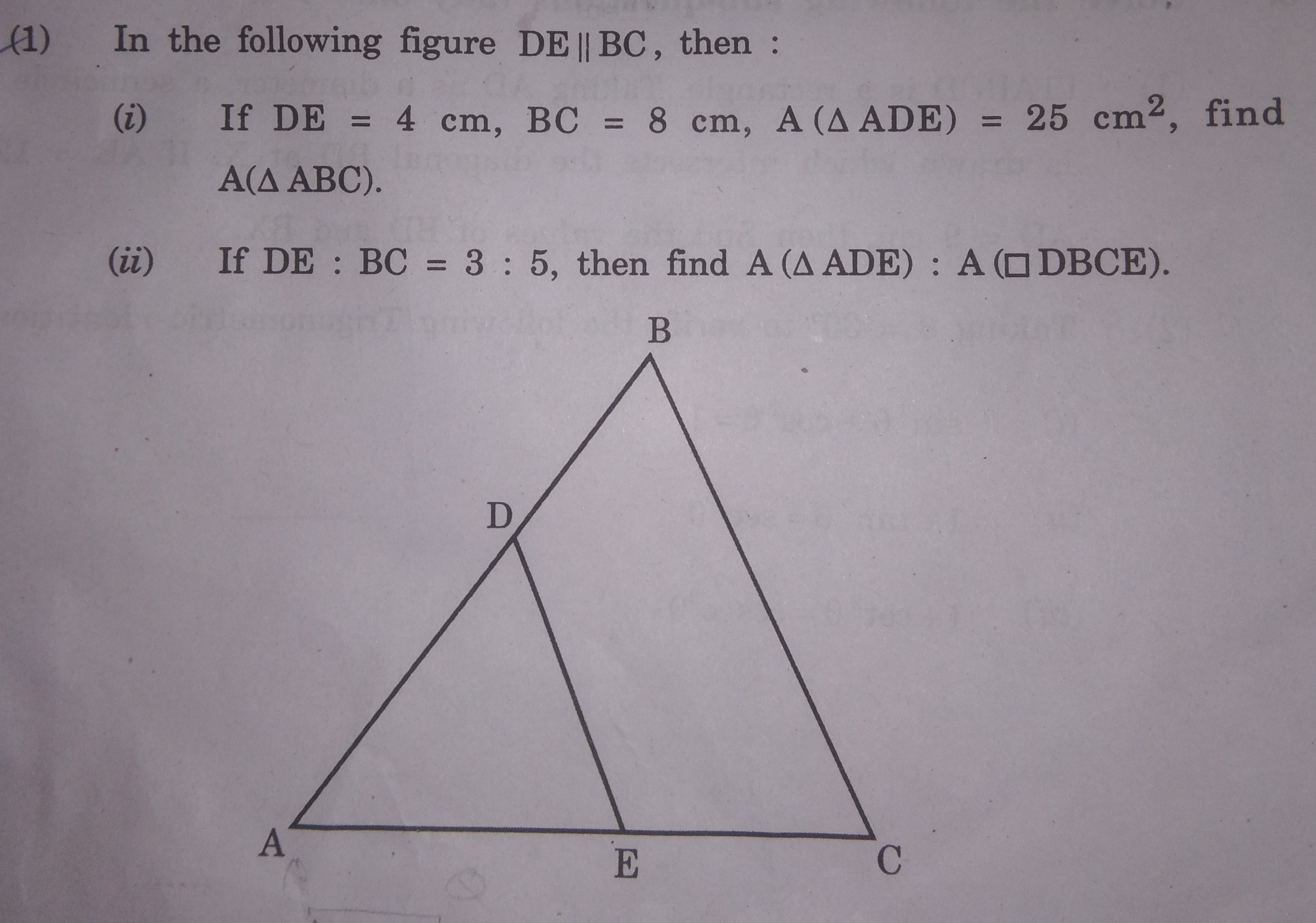
In the following figure DE || BC, then :

(i) If DE = 4 cm, BC = 8 cm, Α (Δ ADE) = 25 $cm^2$, find Α(Δ ABC).

(ii) If DE : BC = 3 : 5, then find A (Δ ADE) : A (□ DBCE).

Answer 1

(i) A(Δ ABC) = 100 $cm^2$ (ii) A(Δ ADE) : A(□ DBCE) = 9 : 16

Answer 2

For both parts, the key is recognizing that since DE || BC, triangle ADE is similar to triangle ABC. The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.

(i) Using the given side lengths DE=4 cm and BC=8 cm, and A(Δ ADE)=25 cm², we set up the ratio of areas: A(Δ ADE)/A(Δ ABC) = (DE/BC)². This simplifies to 25/A(Δ ABC) = (4/8)² = (1/2)² = 1/4. Solving for A(Δ ABC) gives 100 cm².

(ii) Using the given ratio DE:BC = 3:5, we find A(Δ ADE)/A(Δ ABC) = (3/5)² = 9/25. This means A(Δ ADE) is 9 parts and A(Δ ABC) is 25 parts. The area of the quadrilateral DBCE is A(Δ ABC) - A(Δ ADE) = 25 parts - 9 parts = 16 parts. Therefore, the ratio A(Δ ADE) : A(□ DBCE) is 9:16.