Question
Question: If $\sum_{k=1}^{\infty} \frac{1}{k^2} = \frac{\pi^2}{6}$ and $S_i = \sum_{k=1}^{\infty} \frac{i}{(36...
If ∑k=1∞k21=6π2 and Si=∑k=1∞(36k2−1)ii, then S1+S2 is equal to
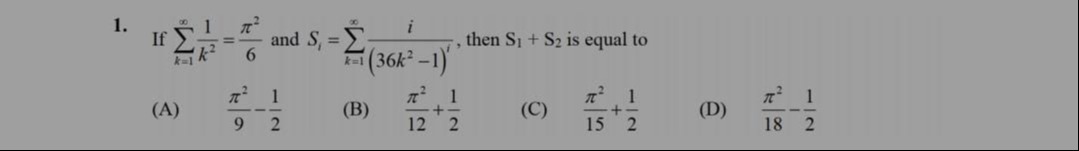
9π2−21
12π2+21
15π2+21
18π2−21
18π2−21
Solution
We are given Si=∑k=1∞(36k2−1)ii. We need to find S1+S2.
Calculating S1: For i=1, S1=∑k=1∞36k2−11. We use the partial fraction decomposition of 36k2−11. 36k2−1=(6k)2−12=(6k−1)(6k+1). 36k2−11=21(6k−11−6k+11) The sum S1 can be related to a known series summation formula: ∑k=1∞k2−a21=2a21−2aπcot(πa) Let a=1/6. Then a2=1/36. ∑k=1∞k2−(1/6)21=∑k=1∞36k2−136=36S1 Using the formula: 36S1=2(1/6)21−2(1/6)πcot(π/6)=2(1/36)1−1/3π3=18−3π3 S1=3618−3π3=21−12π3
Calculating S2: For i=2, S2=∑k=1∞(36k2−1)22=2∑k=1∞(36k2−1)21. S2=2∑k=1∞362(k2−(1/6)2)21=12962∑k=1∞(k2−(1/6)2)21 We use the formula: ∑k=1∞(k2−a2)21=−2a41+4a3πcot(πa)+4a2π2csc2(πa) With a=1/6: a2=1/36, a3=1/216, a4=1/1296. cot(π/6)=3, csc(π/6)=2, csc2(π/6)=4. ∑k=1∞(k2−(1/6)2)21=−2(1/1296)1+4(1/216)π3+4(1/36)π2(4) =−648+54π3+36π2 Now, substitute this back into the expression for S2: S2=12962(−648+54π3+36π2)=6481(−648+54π3+36π2) S2=−1+64854π3+64836π2=−1+12π3+18π2
Calculating S1+S2: S1+S2=(21−12π3)+(−1+12π3+18π2) S1+S2=21−1−12π3+12π3+18π2 S1+S2=−21+18π2
