Question
Question: If $f(x) = \log_e (\frac{x^2+e}{x^2+1})$, then the number of integers in the range of $f(x)$ is...
If f(x)=loge(x2+1x2+e), then the number of integers in the range of f(x) is
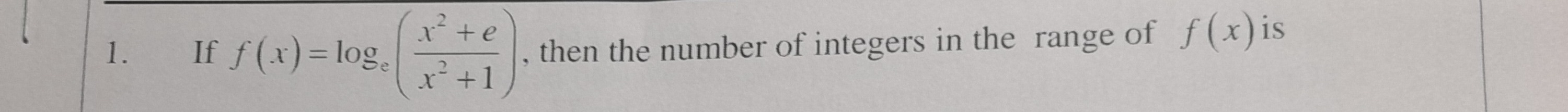
0
1
2
Infinite
1
Solution
The problem asks us to find the number of integers in the range of the function f(x)=loge(x2+1x2+e).
1. Analyze the argument of the logarithm: Let g(x)=x2+1x2+e. To find the range of g(x), let t=x2. Since x is a real number, x2≥0, so t≥0. Now, g(t)=t+1t+e. We can rewrite g(t) by performing polynomial division or by algebraic manipulation: g(t)=t+1t+1+e−1=t+1t+1+t+1e−1=1+t+1e−1.
2. Determine the range of g(t) for t≥0: Since t≥0: t+1≥1. Taking the reciprocal of t+1: 0<t+11≤1. (As t→∞, t+11→0. When t=0, t+11=1).
The value of e is approximately 2.718. So, e−1≈1.718, which is a positive constant. Multiply the inequality 0<t+11≤1 by (e−1): 0⋅(e−1)<t+1e−1≤1⋅(e−1) 0<t+1e−1≤e−1.
Now, add 1 to all parts of the inequality: 1+0<1+t+1e−1≤1+(e−1) 1<g(t)≤e.
So, the range of g(x)=x2+1x2+e is (1,e].
3. Find the range of f(x)=loge(g(x)): The natural logarithm function, h(u)=logeu, is a strictly increasing function for u>0. Since the range of g(x) is (1,e], we can apply the logarithm to this interval: loge(1)<loge(g(x))≤loge(e). We know that loge(1)=0 and loge(e)=1. Therefore, the range of f(x) is (0,1].
4. Count the number of integers in the range of f(x): The range of f(x) is (0,1]. The integers that lie within this interval are values greater than 0 and less than or equal to 1. The only integer satisfying this condition is 1.
Thus, there is only one integer in the range of f(x).
