Question

If f be a continuous function on [0, 1], differentiable in (0, 1) such that f(1) = 0, then their exists some $c \in (0,1)$ such that:

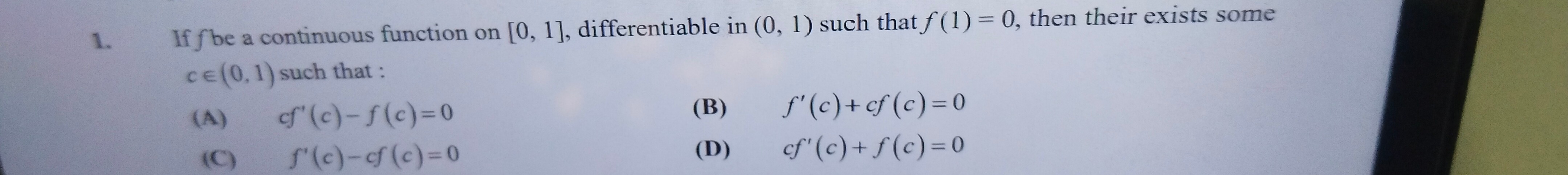
• A. cf'(c) - f(c) = 0
• B. f'(c) + cf(c) = 0
• C. f'(c) - cf(c) = 0
• D. cf'(c) + f(c) = 0

Answer 1

Answer: (D)

cf'(c) + f(c) = 0

Answer 2

To solve this problem, we can construct an auxiliary function and apply Rolle's Theorem. Let $g(x) = xf(x)$.

1. Continuity of $g(x)$: Since $f(x)$ is continuous on $[0,1]$ and $x$ is continuous on $[0,1]$, their product $g(x) = xf(x)$ is continuous on $[0,1]$.
2. Differentiability of $g(x)$: Since $f(x)$ is differentiable on $(0,1)$ and $x$ is differentiable on $(0,1)$, their product $g(x) = xf(x)$ is differentiable on $(0,1)$. The derivative is $g'(x) = \frac{d}{dx}(xf(x)) = 1 \cdot f(x) + x \cdot f'(x) = f(x) + xf'(x)$.
3. Equality of function values at endpoints: At $x=0$, $g(0) = 0 \cdot f(0) = 0$ (since $f(0)$ is finite due to continuity). At $x=1$, $g(1) = 1 \cdot f(1)$. Given $f(1)=0$, so $g(1) = 1 \cdot 0 = 0$. Thus, $g(0) = g(1) = 0$.

Since $g(x)$ satisfies the conditions of Rolle's Theorem on $[0,1]$, there exists some $c \in (0,1)$ such that $g'(c) = 0$. Substituting the expression for $g'(c)$: $f(c) + cf'(c) = 0$

This equation matches option (D).

We can verify this with an example. Let $f(x) = 1-x$. This function is continuous on $[0,1]$, differentiable on $(0,1)$, and $f(1)=0$. Its derivative is $f'(x)=-1$. For option (D): $c(-1) + (1-c) = -c + 1 - c = 1 - 2c$. Setting this to 0 gives $c=1/2$, which is in $(0,1)$. This confirms option (D) is a valid condition.