Solveeit Logo
Login

Question

Question: If $2sin^{-1}x = sin^{-1}(2x\sqrt{1-x^2})$, then x belongs to:...

If 2sin−1x=sin−1(2x1−x2)2sin^{-1}x = sin^{-1}(2x\sqrt{1-x^2}), then x belongs to:

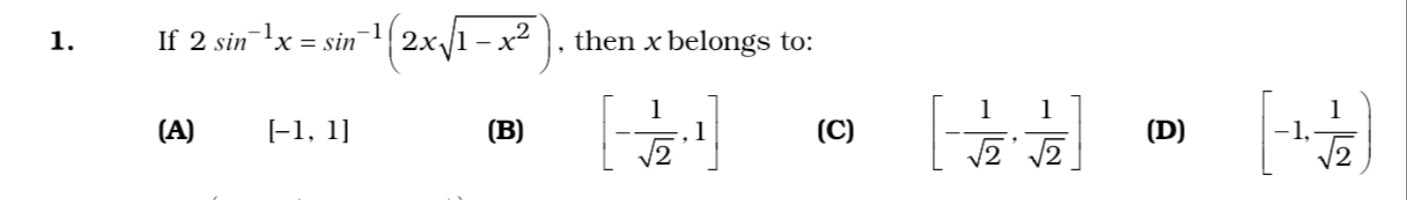
A

[-1, 1]

B

[-\frac{1}{\sqrt{2}}, 1]

C

[-\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}]

D

[-1, \frac{1}{\sqrt{2}})

Answer

[-\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}]

Explanation

Solution

Let x=sin⁡θx = \sin\theta, where θ∈[−π2,π2]\theta \in [-\frac{\pi}{2}, \frac{\pi}{2}]. The equation 2sin⁡−1x=sin⁡−1(2x1−x2)2\sin^{-1}x = \sin^{-1}(2x\sqrt{1-x^2}) transforms to 2θ=sin⁡−1(sin⁡(2θ))2\theta = \sin^{-1}(\sin(2\theta)). The identity sin⁡−1(sin⁡ϕ)=ϕ\sin^{-1}(\sin\phi) = \phi holds if and only if ϕ∈[−π2,π2]\phi \in [-\frac{\pi}{2}, \frac{\pi}{2}]. Applying this to 2θ2\theta, we require 2θ∈[−π2,π2]2\theta \in [-\frac{\pi}{2}, \frac{\pi}{2}]. This implies θ∈[−π4,π4]\theta \in [-\frac{\pi}{4}, \frac{\pi}{4}]. Since x=sin⁡θx = \sin\theta and sin⁡θ\sin\theta is strictly increasing for θ∈[−π2,π2]\theta \in [-\frac{\pi}{2}, \frac{\pi}{2}], the range for xx is: x∈[sin⁡(−π4),sin⁡(π4)]=[−12,12]x \in [\sin(-\frac{\pi}{4}), \sin(\frac{\pi}{4})] = [-\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}].