Solveeit Logo
Login

Question

Question: $1-\frac{2}{t+\frac{1}{t}+1}$...

1−2t+1t+11-\frac{2}{t+\frac{1}{t}+1}

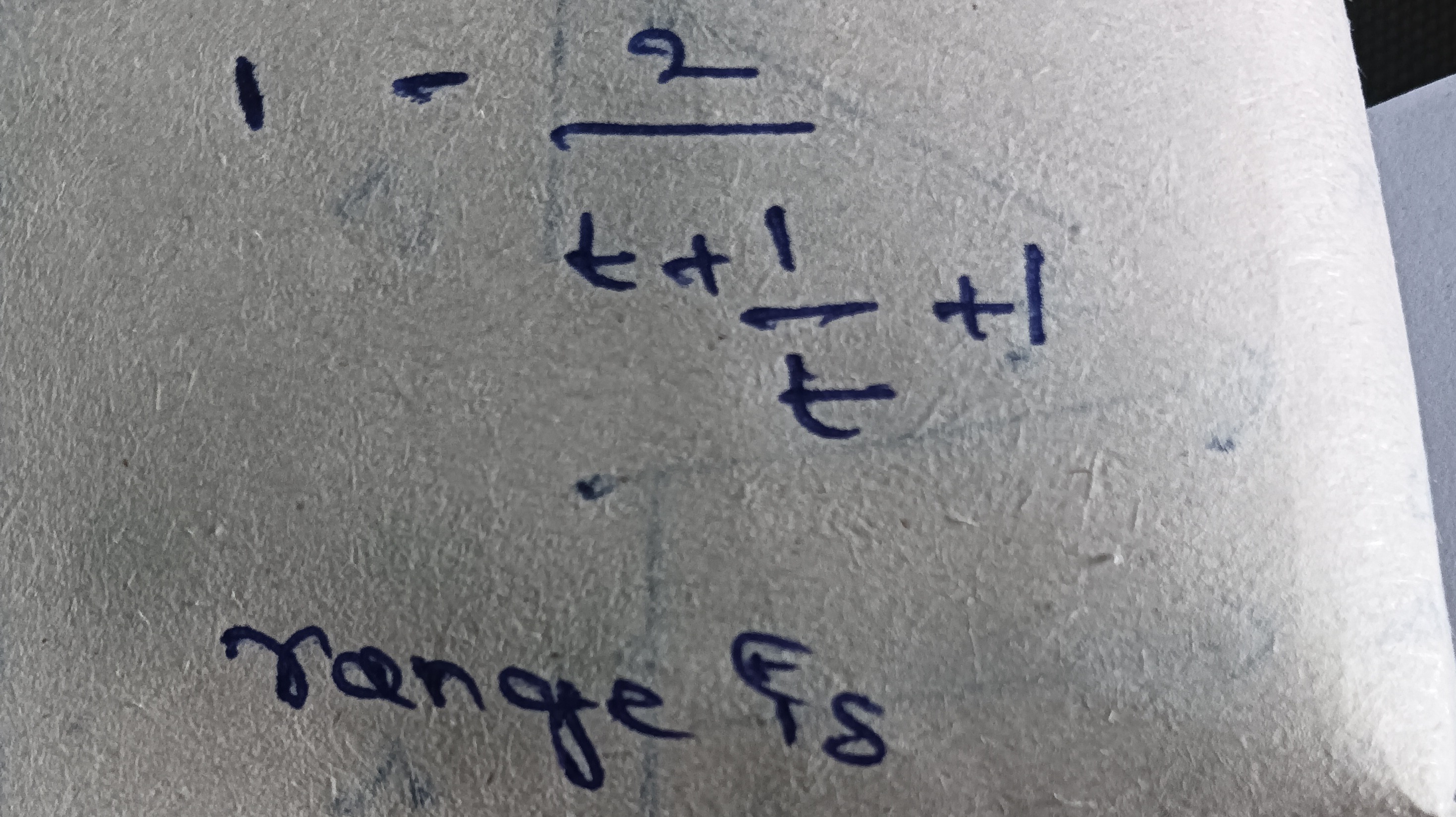
Answer

The range of the expression 1−2t+1t+11-\frac{2}{t+\frac{1}{t}+1} is [13,1)∪(1,3][\frac{1}{3}, 1) \cup (1, 3].

Explanation

Solution

Let the given expression be EE. E=1−2t+1t+1E = 1-\frac{2}{t+\frac{1}{t}+1}

We assume tt is a real number and t≠0t \neq 0 for the expression to be defined.

  1. Analyze the term y=t+1ty = t + \frac{1}{t}:

    • For t>0t > 0, by AM-GM inequality, t+1t≥2t⋅1t=2t + \frac{1}{t} \ge 2\sqrt{t \cdot \frac{1}{t}} = 2. The minimum value is 2 (at t=1t=1). As t→0+t \to 0^+ or t→∞t \to \infty, y→∞y \to \infty. So, for t>0t>0, y∈[2,∞)y \in [2, \infty).
    • For t<0t < 0, let t=−ut = -u where u>0u > 0. Then y=−u−1u=−(u+1u)y = -u - \frac{1}{u} = -(u + \frac{1}{u}). Since u+1u≥2u + \frac{1}{u} \ge 2, we have y≤−2y \le -2. The maximum value is -2 (at t=−1t=-1). As t→0−t \to 0^- or t→−∞t \to -\infty, y→−∞y \to -\infty. So, for t<0t<0, y∈(−∞,−2]y \in (-\infty, -2].
    • Combining both cases, the range of y=t+1ty = t + \frac{1}{t} is (−∞,−2]∪[2,∞)(-\infty, -2] \cup [2, \infty).

  2. Analyze the denominator D=t+1t+1D = t + \frac{1}{t} + 1:

    • Let D=y+1D = y + 1.
    • If y∈[2,∞)y \in [2, \infty), then D∈[2+1,∞+1)=[3,∞)D \in [2+1, \infty+1) = [3, \infty).
    • If y∈(−∞,−2]y \in (-\infty, -2], then D∈(−∞+1,−2+1]=(−∞,−1]D \in (-\infty+1, -2+1] = (-\infty, -1].
    • The range of DD is (−∞,−1]∪[3,∞)(-\infty, -1] \cup [3, \infty). Note that DD is never zero for real tt, as t2+t+1=0t^2+t+1=0 has no real roots.

  3. Analyze the term 2D\frac{2}{D}:

    • If D∈[3,∞)D \in [3, \infty): As DD ranges from 33 to ∞\infty, 1D\frac{1}{D} ranges from 13\frac{1}{3} to 00. Thus, 2D∈(0,23]\frac{2}{D} \in (0, \frac{2}{3}].
    • If D∈(−∞,−1]D \in (-\infty, -1]: As DD ranges from −∞-\infty to −1-1, 1D\frac{1}{D} ranges from 00 to −1-1. Thus, 2D∈[−2,0)\frac{2}{D} \in [-2, 0).
    • The range of 2D\frac{2}{D} is [−2,0)∪(0,23][-2, 0) \cup (0, \frac{2}{3}].

  4. Analyze the expression E=1−2DE = 1 - \frac{2}{D}:

    • If 2D∈(0,23]\frac{2}{D} \in (0, \frac{2}{3}]: E=1−(a value in (0,23])E = 1 - (\text{a value in } (0, \frac{2}{3}]). The range is [1−23,1−0)=[13,1)[1-\frac{2}{3}, 1-0) = [\frac{1}{3}, 1).
    • If 2D∈[−2,0)\frac{2}{D} \in [-2, 0): E=1−(a value in [−2,0))E = 1 - (\text{a value in } [-2, 0)). The range is (1−0,1−(−2)]=(1,3](1-0, 1-(-2)] = (1, 3].

  5. Combine the ranges: The total range of the expression EE is the union of the ranges from the two cases: [13,1)∪(1,3][\frac{1}{3}, 1) \cup (1, 3].