Question
Question: $\frac{15-4x}{x^{2}-x-12}<4$...
x2−x−1215−4x<4
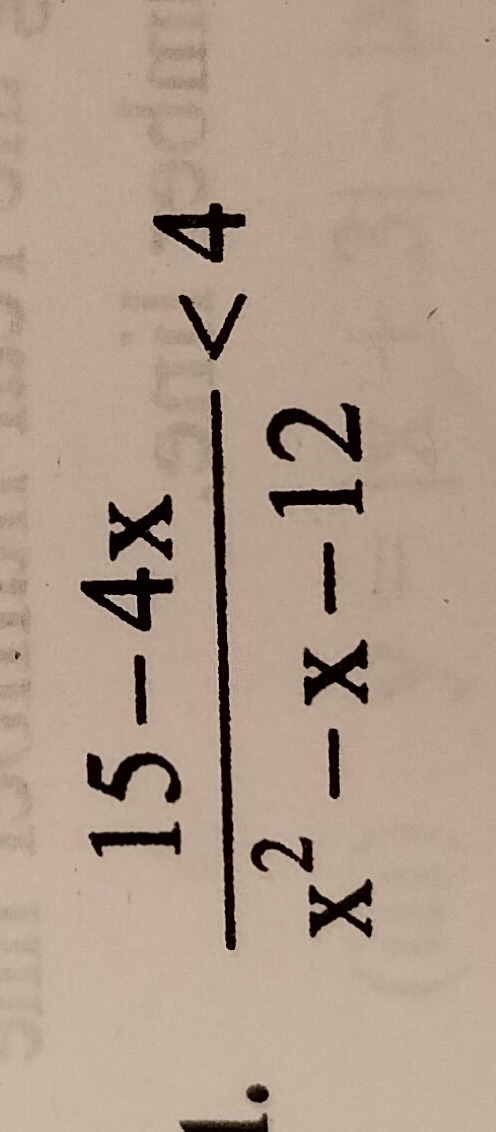
(−∞,−237)∪(−3,237)∪(4,∞)
Solution
The given inequality is x2−x−1215−4x<4.
Step 1: Move all terms to one side to get a zero on the other side. x2−x−1215−4x−4<0
Step 2: Find a common denominator and combine the terms into a single fraction. The denominator is x2−x−12. Factoring the denominator, we get x2−x−12=(x−4)(x+3). So, the inequality is (x−4)(x+3)15−4x−4<0. The common denominator is (x−4)(x+3). (x−4)(x+3)15−4x−4(x−4)(x+3)<0 Expand the term 4(x−4)(x+3): 4(x−4)(x+3)=4(x2+3x−4x−12)=4(x2−x−12)=4x2−4x−48. Substitute this back into the inequality: (x−4)(x+3)15−4x−(4x2−4x−48)<0 (x−4)(x+3)15−4x−4x2+4x+48<0 (x−4)(x+3)−4x2+63<0
Step 3: Multiply by -1 and reverse the inequality sign. (x−4)(x+3)4x2−63>0
Step 4: Find the critical points by setting the numerator and the denominator equal to zero. Numerator: 4x2−63=0⟹4x2=63⟹x2=463⟹x=±463=±29×7=±237. The roots of the numerator are x=−237 and x=237.
Denominator: (x−4)(x+3)=0⟹x−4=0 or x+3=0⟹x=4 or x=−3. The roots of the denominator are x=−3 and x=4.
The critical points, in increasing order, are −237, −3, 237, 4. Approximate values: 7≈2.646, so 237≈23×2.646≈27.938≈3.969. The ordered critical points are approximately −3.969,−3,3.969,4.
Step 5: Analyze the sign of the expression (x−4)(x+3)4x2−63 in the intervals defined by the critical points. The critical points divide the number line into five intervals: (−∞,−237), (−237,−3), (−3,237), (237,4), (4,∞).
Let f(x)=(x−4)(x+3)4x2−63. We need to find where f(x)>0. We can use the sign chart method or test points in each interval. The expression is (x−4)(x+3)4(x−237)(x+237).
- Interval (−∞,−237): Choose x=−5. f(−5)=(−5−4)(−5+3)4(−5)2−63=(−9)(−2)100−63=1837>0.
- Interval (−237,−3): Choose x=−3.5. f(−3.5)=(−3.5−4)(−3.5+3)4(−3.5)2−63=(−7.5)(−0.5)4(12.25)−63=3.7549−63=3.75−14<0.
- Interval (−3,237): Choose x=0. f(0)=(0−4)(0+3)4(0)2−63=(−4)(3)−63=−12−63=421>0.
- Interval (237,4): Choose x=3.9. f(3.9)=(3.9−4)(3.9+3)4(3.9)2−63=(−0.1)(6.9)4(15.21)−63=−0.6960.84−63=−0.69−2.16>0.
The intervals where f(x)>0 are (−∞,−237), (−3,237), and (4,∞). The points where the denominator is zero (x=−3 and x=4) must be excluded from the solution. The points where the numerator is zero (x=±237) are also excluded because the inequality is strict (>0).
The solution set is the union of these intervals: x∈(−∞,−237)∪(−3,237)∪(4,∞).
