Question
Question: $\frac{15-4x}{x^{2}-x-12}<4$...
x2−x−1215−4x<4
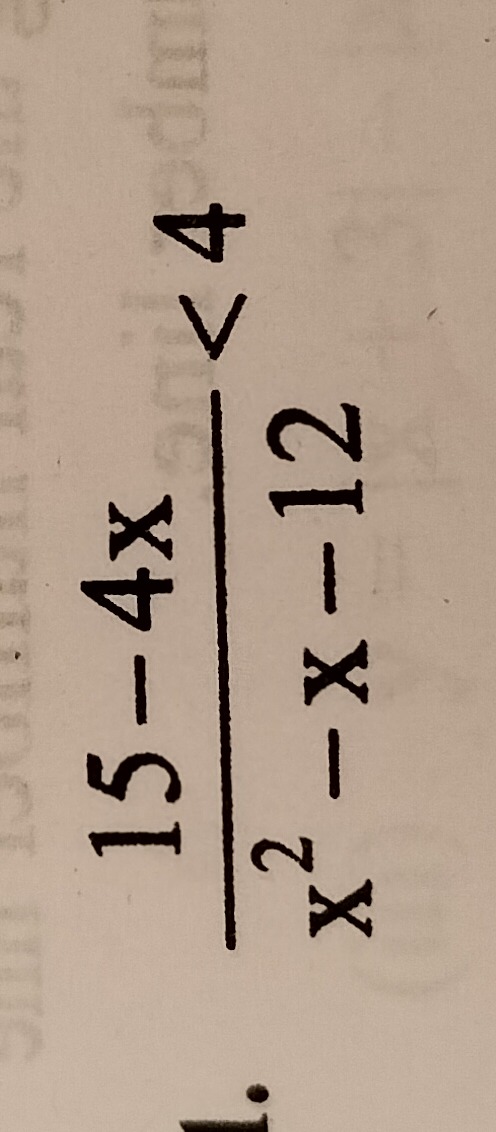
x∈(−∞,−237)∪(−3,237)∪(4,∞)
Solution
To solve the inequality x2−x−1215−4x<4, follow these steps:
-
Move all terms to one side:
x2−x−1215−4x−4<0
-
Combine into a single fraction:
x2−x−1215−4x−4(x2−x−12)<0
x2−x−1215−4x−4x2+4x+48<0
x2−x−12−4x2+63<0
-
Multiply by -1 and reverse the inequality:
x2−x−124x2−63>0
-
Factor the numerator and denominator:
Numerator: 4x2−63=(2x−37)(2x+37)
Denominator: x2−x−12=(x−4)(x+3)
So the inequality becomes:
(x−4)(x+3)(2x−37)(2x+37)>0
-
Find critical points:
Numerator: x=±237
Denominator: x=4,x=−3
-
Arrange critical points in increasing order:
−237≈−3.9675,−3,237≈3.9675,4
-
Determine the sign of the expression in each interval:
- (−∞,−237): Positive
- (−237,−3): Negative
- (−3,237): Positive
- (237,4): Negative
- (4,∞): Positive
-
Identify intervals where the expression is greater than 0:
(−∞,−237)∪(−3,237)∪(4,∞)
Thus, the solution is x∈(−∞,−237)∪(−3,237)∪(4,∞).
