Question
Question: $\frac{15-4x}{x^2-x-12} < 4$...
x2−x−1215−4x<4
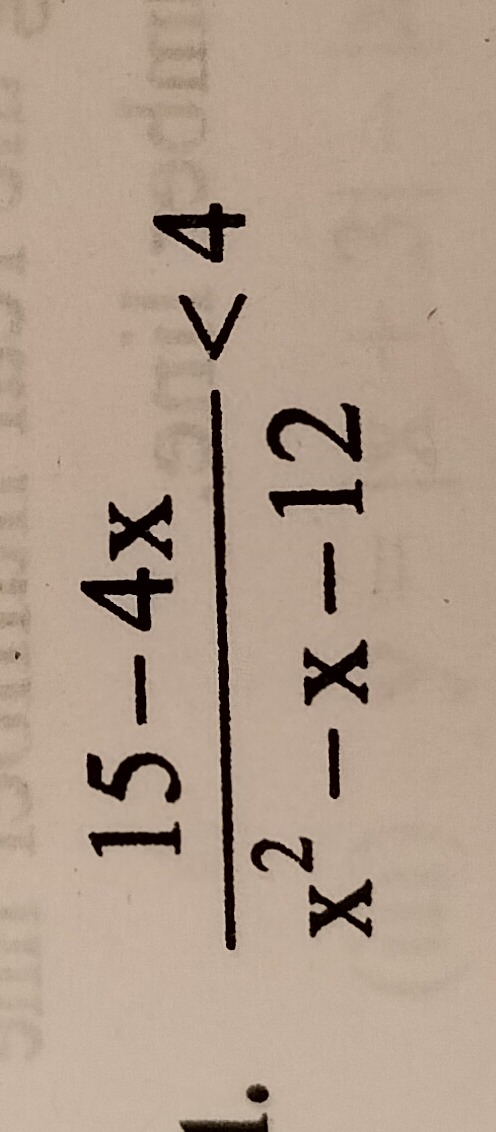
Answer
(−∞,−237)∪(−3,237)∪(4,∞)
Explanation
Solution
To solve the inequality x2−x−1215−4x<4:
-
Move all terms to one side: x2−x−1215−4x−4<0
-
Find a common denominator: x2−x−1215−4x−4(x2−x−12)<0
-
Expand and simplify the numerator: x2−x−1215−4x−4x2+4x+48<0 x2−x−12−4x2+63<0
-
Multiply by -1 to make the leading coefficient positive (and reverse the inequality): x2−x−124x2−63>0
-
Find the roots of the numerator and denominator:
- Numerator: 4x2−63=0⟹x=±237≈±3.969
- Denominator: x2−x−12=0⟹(x−4)(x+3)=0⟹x=4,−3
-
The critical points are −237≈−3.969, −3, 237≈3.969, and 4.
-
Test intervals: (−∞,−237), (−237,−3), (−3,237), (237,4), (4,∞).
-
Determine the sign of the expression in each interval:
- (−∞,−237): Positive
- (−237,−3): Negative
- (−3,237): Positive
- (237,4): Negative
- (4,∞): Positive
-
Since we want the expression to be greater than 0, the solution is (−∞,−237)∪(−3,237)∪(4,∞).
