Question

$1-\frac{1}{3^2} + \frac{1}{5^2} - \frac{1}{7^2} + ...$

Answer 1

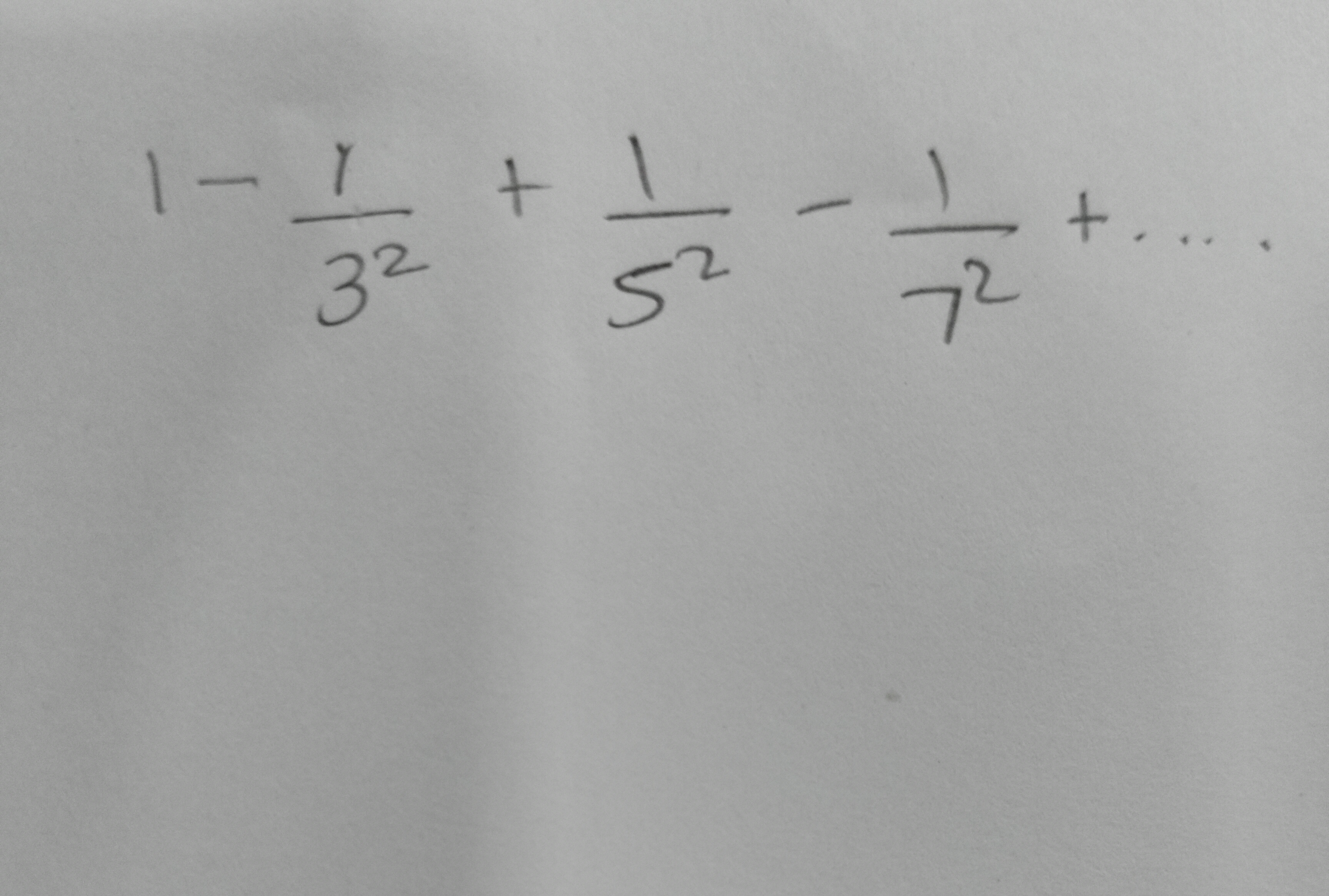
G (Catalan's Constant)

Answer 2

The given series is $S = 1-\frac{1}{3^2} + \frac{1}{5^2} - \frac{1}{7^2} + ...$.

This can be written in summation notation as:

$S = \sum_{n=0}^{\infty} \frac{(-1)^n}{(2n+1)^2}$

This series is a well-known mathematical constant called Catalan's Constant, often denoted by $G$.

One way to derive this series is by integrating the Maclaurin series for $\arctan(x)$. The Maclaurin series for $\arctan(x)$ for $|x| \le 1$ is:

$\arctan(x) = x - \frac{x^3}{3} + \frac{x^5}{5} - \frac{x^7}{7} + \dots$

Divide both sides by $x$:

$\frac{\arctan(x)}{x} = 1 - \frac{x^2}{3} + \frac{x^4}{5} - \frac{x^6}{7} + \dots$

Now, integrate both sides from $0$ to $1$:

$\int_0^1 \frac{\arctan(x)}{x} dx = \int_0^1 \left(1 - \frac{x^2}{3} + \frac{x^4}{5} - \frac{x^6}{7} + \dots \right) dx$

Integrating term by term:

$= \left[ x - \frac{x^3}{3 \cdot 3} + \frac{x^5}{5 \cdot 5} - \frac{x^7}{7 \cdot 7} + \dots \right]_0^1$

$= \left[ x - \frac{x^3}{3^2} + \frac{x^5}{5^2} - \frac{x^7}{7^2} + \dots \right]_0^1$

Evaluating at the limits:

$= \left( 1 - \frac{1}{3^2} + \frac{1}{5^2} - \frac{1}{7^2} + \dots \right) - (0)$

Thus, the sum of the given series is equal to the definite integral $\int_0^1 \frac{\arctan(x)}{x} dx$.

This integral is the definition of Catalan's Constant, $G$.

Catalan's Constant is not known to have a simple closed-form expression in terms of elementary constants like $\pi$ or $e$. Its approximate numerical value is $G \approx 0.91596559$.

The final answer is $G \text{ (Catalan's Constant)}$.