Question
Question: $\frac{1}{1+1^2+1^4}+\frac{2}{1+2^2+2^4}+\frac{3}{1+3^2+3^4}+...=H/w$...
1+12+141+1+22+242+1+32+343+...=H/w
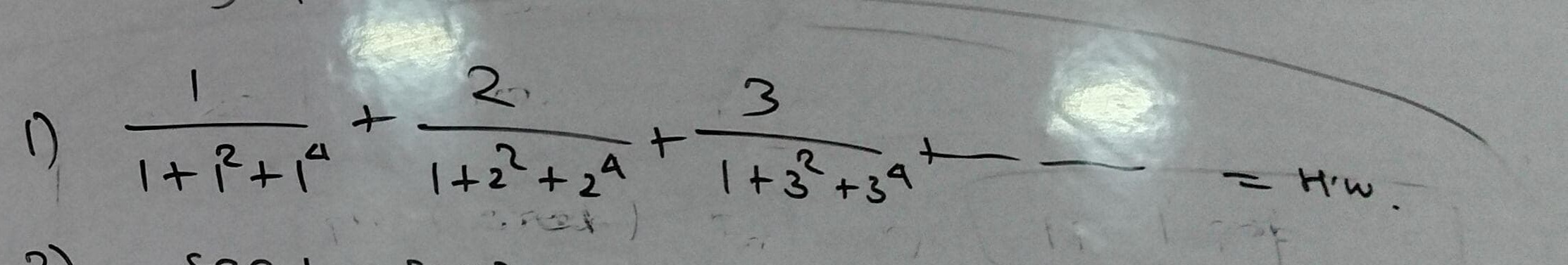
1/2
Solution
The problem asks to find the sum of the infinite series:
S=∑n=1∞1+n2+n4n
Let's analyze the general term of the series, Tn=1+n2+n4n.
Step 1: Factorize the denominator
The denominator 1+n2+n4 can be factorized using the identity a4+a2+1=(a2+1)2−a2=(a2+1−a)(a2+1+a). So, 1+n2+n4=(n2−n+1)(n2+n+1).
Step 2: Rewrite the general term as a difference of two terms
Substitute the factorization back into Tn:
Tn=(n2−n+1)(n2+n+1)n
Notice that the difference between the two factors in the denominator is (n2+n+1)−(n2−n+1)=2n. To utilize this, multiply and divide Tn by 2:
Tn=21(n2−n+1)(n2+n+1)2n
Now, replace 2n with the difference of the factors:
Tn=21(n2−n+1)(n2+n+1)(n2+n+1)−(n2−n+1)
This can be split into two fractions:
Tn=21(n2−n+11−n2+n+11)
Step 3: Identify the telescoping sum pattern
Let f(n)=n2−n+11. Then, let's evaluate f(n+1):
f(n+1)=(n+1)2−(n+1)+11=n2+2n+1−n−1+11=n2+n+11
So, the general term Tn can be written as:
Tn=21(f(n)−f(n+1))
Step 4: Calculate the partial sum SN
The sum of the first N terms is SN=∑n=1NTn:
SN=∑n=1N21(f(n)−f(n+1)) SN=21[(f(1)−f(2))+(f(2)−f(3))+(f(3)−f(4))+⋯+(f(N)−f(N+1))]
This is a telescoping sum where intermediate terms cancel out:
SN=21[f(1)−f(N+1)]
Step 5: Evaluate f(1) and f(N+1)
f(1)=12−1+11=11=1 f(N+1)=(N+1)2−(N+1)+11=N2+N+11
Substitute these values back into SN:
SN=21[1−N2+N+11]
Step 6: Find the sum of the infinite series
The sum of the infinite series S is the limit of SN as N→∞:
S=limN→∞SN=limN→∞21[1−N2+N+11]
As N→∞, the term N2+N+11 approaches 0.
S=21[1−0]=21
The sum of the given series is 21.
