Question

For the reaction: xA $\rightarrow$ yB, $\log_{10}(-\frac{d[A]}{dt}) = \log_{10}(+\frac{d[B]}{dt})+0.3$

If the value of $\log_{10}5 = 0.7$, the value of x : y is :

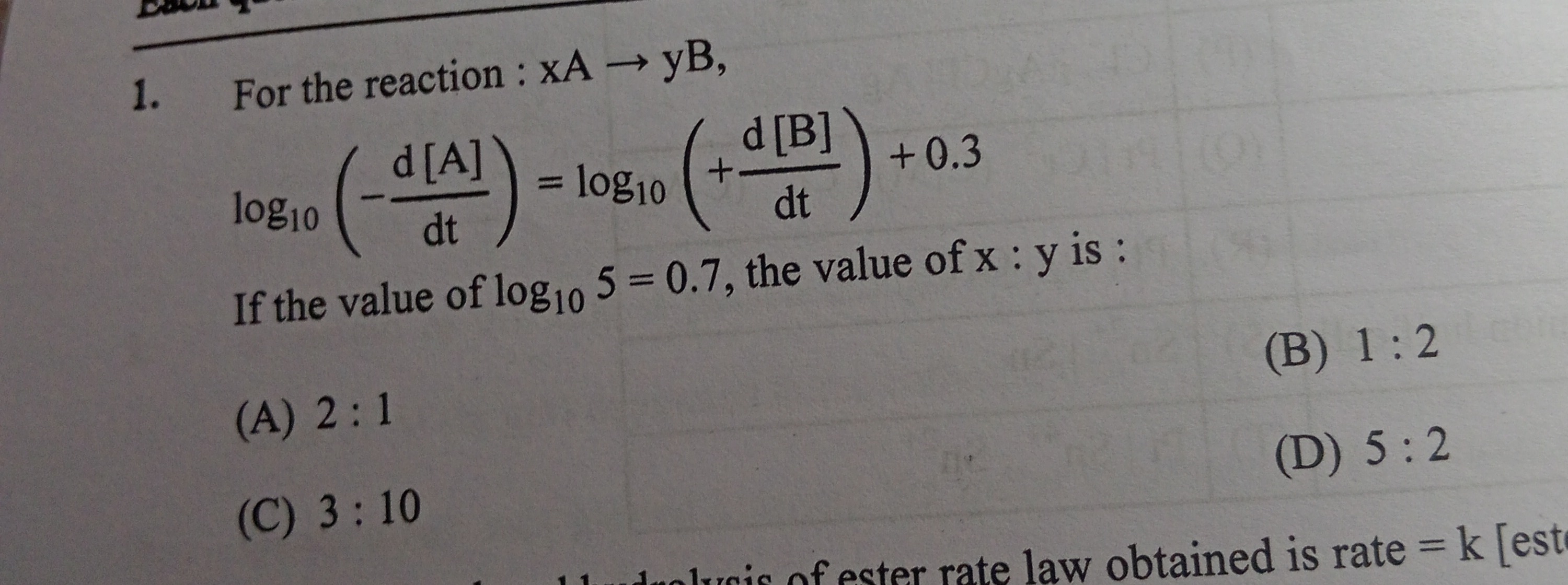
• A. 2 : 1
• B. 1 : 2
• C. 3 : 10
• D. 5 : 2

Answer 1

Answer: (A)

2 : 1

Answer 2

The rate of the reaction xA $\rightarrow$ yB can be expressed in terms of the rate of disappearance of A and the rate of appearance of B using the stoichiometric coefficients:

Rate $= -\frac{1}{x}\frac{d[A]}{dt} = +\frac{1}{y}\frac{d[B]}{dt}$

From this relationship, we can write:

$-\frac{d[A]}{dt} = \frac{x}{y}\left(+\frac{d[B]}{dt}\right)$

The problem gives a logarithmic relationship between the rates:

$\log_{10}\left(-\frac{d[A]}{dt}\right) = \log_{10}\left(+\frac{d[B]}{dt}\right)+0.3$

Substitute the expression for $-\frac{d[A]}{dt}$ from the stoichiometric relationship into the given equation:

$\log_{10}\left(\frac{x}{y}\left(+\frac{d[B]}{dt}\right)\right) = \log_{10}\left(+\frac{d[B]}{dt}\right)+0.3$

Using the logarithm property $\log(AB) = \log A + \log B$:

$\log_{10}\left(\frac{x}{y}\right) + \log_{10}\left(+\frac{d[B]}{dt}\right) = \log_{10}\left(+\frac{d[B]}{dt}\right)+0.3$

Subtract $\log_{10}\left(+\frac{d[B]}{dt}\right)$ from both sides of the equation:

$\log_{10}\left(\frac{x}{y}\right) = 0.3$

We are given that $\log_{10}5 = 0.7$. We know that $\log_{10}10 = 1$. Using the logarithm property $\log(A/B) = \log A - \log B$:

$\log_{10}2 = \log_{10}\left(\frac{10}{5}\right) = \log_{10}10 - \log_{10}5 = 1 - 0.7 = 0.3$

So, the constant 0.3 is equal to $\log_{10}2$. Substitute this back into the equation for $\frac{x}{y}$:

$\log_{10}\left(\frac{x}{y}\right) = \log_{10}2$

Since the logarithms are equal and the base is the same, the arguments must be equal:

$\frac{x}{y} = 2$

This means the ratio x : y is 2 : 1.