Question

Find two unit vectors each of which is perpendicular to both $\bar{u}$ and $\bar{v}$, where $\bar{u} = 2\hat{i} + \hat{j} - 2\hat{k}, \bar{v} = \hat{i} + 2\hat{j} - 2\hat{k}$

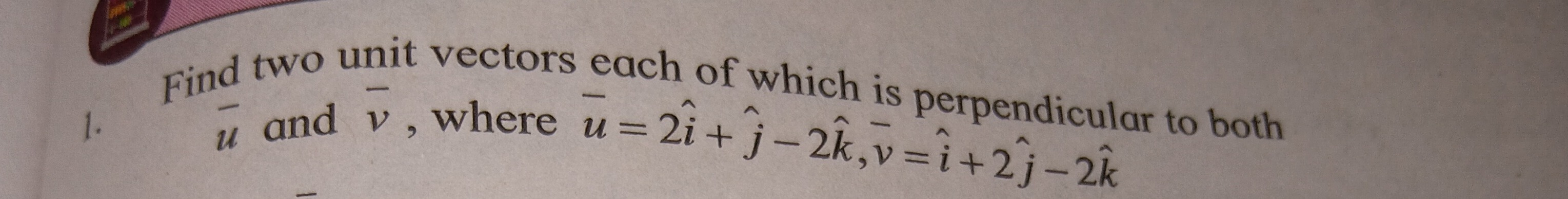
Answer 1

$\pm \frac{1}{\sqrt{17}}\langle 2, 2, 3 \rangle$

Answer 2

Step 1. Find the Cross Product

The unit vectors perpendicular to both u and v are along the direction of u × v. Given

$$\mathbf{u} = \langle2, 1,-2\rangle \quad \text{and} \quad \mathbf{v} = \langle1, 2,-2\rangle,$$

the cross product is:

$$\mathbf{u}\times\mathbf{v} = \langle u_{2}v_{3} - u_{3}v_{2}, u_{3}v_{1} - u_{1}v_{3}, u_{1}v_{2} - u_{2}v_{1} \rangle.$$

Calculating each component:

• $x$-component: $1\cdot(-2) - (-2)\cdot2 = -2 + 4 = 2$,
• $y$-component: $(-2)\cdot1 - 2\cdot(-2) = -2 + 4 = 2$,
• $z$-component: $2\cdot2 - 1\cdot1 = 4 - 1 = 3$.

Thus,

$$\mathbf{u}\times\mathbf{v} = \langle 2, 2, 3 \rangle.$$

Step 2. Find the Unit Vectors

The magnitude of $\mathbf{u}\times\mathbf{v}$ is:

$$\|\mathbf{u}\times\mathbf{v}\| = \sqrt{2^2 + 2^2 + 3^2} = \sqrt{4+4+9} = \sqrt{17}.$$

The unit vector in the direction of $\mathbf{u}\times\mathbf{v}$ is:

$$\mathbf{\hat{n}} = \frac{1}{\sqrt{17}}\langle 2, 2, 3 \rangle.$$

Since both $\mathbf{\hat{n}}$ and $-\mathbf{\hat{n}}$ are perpendicular to both $\mathbf{u}$ and $\mathbf{v}$, the two required unit vectors are:

$$\pm \frac{1}{\sqrt{17}}\langle 2, 2, 3 \rangle.$$