Question

(1) Find the total work by the gas during process A-B-C.
(2) Find $\Delta {U_{A - B - C}}$ if the gas is monatomic.

Answer 1

Here, a process is carried out on the gas so that the configuration of the parameters is changed. By configuration what is meant is pressure, volume and temperature are changed. You are asked to find the total work done by the gas during process A-B-C, that is work that will be done by the gas to change it configuration from point A to point C through point B. By point what is meant is that what was the configuration (pressure, volume and temperature) of the gas at that point. You can write work in terms of pressure and volume and you're given a graph of pressure versus volume, think of what can be done in order to find the work. Also, use the expression of change in internal energy of a gas.

Complete step by step answer:
Consider a cylinder fitted with a movable piston and the cylinder is filled with some gas. Now, you change the pressure of the gas too slowly so that the pressure applied by you and the pressure of the gas is equal. Infinitesimal work done by a gas is given by $dW = PdV$, so the net work done by the gas will be $\int {dW = \int {PdV} }$. Let us see, why is it so. Let the area of the cross section of the cylinder be $A$. When the piston is moved by an infinitesimal distance $dx$, the work done by the gas will be $dW = Fdx$.

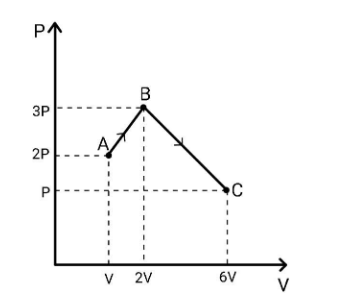
The pressure of the gas will be equal to the pressure applied by the gas on the piston and is given by force per unit area, mathematically, we have $P = \dfrac{F}{A} \to F = PA$. We substitute this in the work formula and then get $dW = PAdx = P\left( {Adx} \right)$. Here, the term $Adx$ is simply the change in volume occurred and hence we write $dW = PdV$ and hence the total work $W = \int {dW = \int {PdV} }$. This you can figure out that it is the area under the P vs V curve. Now, we come back to our question. The total work done will be given by the area under the curve ABC. Therefore,
${W_{A - B - C}} = \dfrac{1}{2}\left( {2P + 3P} \right)\left( {2V - V} \right) + \dfrac{1}{2}\left( {3P + P} \right)\left( {6V - 2V} \right) \\\ \Rightarrow{W_{A - B - C}} = \dfrac{{5PV}}{2} + \dfrac{{16PV}}{2} \\\ \Rightarrow{W_{A - B - C}} = \dfrac{{21PV}}{2} \\\$
Now, the change in internal energy in terms of $\gamma$ (the ratio of specific heats) is given as $\Delta U = \dfrac{{{P_f}{V_f} - {P_i}{V_i}}}{{\gamma - 1}}$. For process A-B-C, we get
$\Delta {U_{A - B - C}} = \dfrac{{\left( P \right)\left( {6V} \right) - \left( {2P} \right)\left( V \right)}}{{\dfrac{5}{3} - 1}} \\\ \therefore\Delta {U_{A - B - C}} = 6PV \\\$
Hence, the work done by the gas is equal to ${W_{A - B - C}} = \dfrac{{21PV}}{2}$ and the change in internal energy is given by $\Delta {U_{A - B - C}} = 6PV$.

Note: We should keep in mind that the value of $\gamma$ for a monatomic gas is given by $\gamma = \dfrac{5}{3}$, if it was a diatomic gas, we would have $\gamma = \dfrac{7}{5}$ and for polyatomic gas, we take $\gamma = \dfrac{4}{3}$. Remember the way we derived the work done by the gas and we have taken the process to be very slow so that the external pressure is equal to the pressure of the gas. Also remember the expression of change in internal energy of the gas. Note that it will be different for different types of gas.