Question

Find the equation of common tangent(s) of (i) $y^2 = 4ax$ and $x^2 = 4by$ (ii) $x^2 + y^2 = 4ax$ and $y^2 = 4ax$ (iii) $x^2 = -8y$ and $y^2 = -x$ (iv) $(x-3)^2 + y^2 = 9$ and $y^2 = 4x

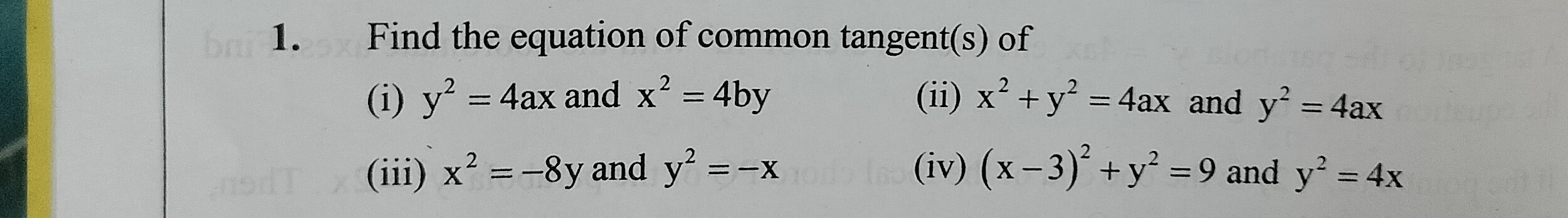
• A. (i) $(a/b)^{1/3} x + y + a(b/a)^{1/3} = 0$, (ii) $x = 0$, (iii) $x + 2y - 1 = 0$, (iv) $x = 0$, $x - \sqrt{3}y + 3 = 0$, $x + \sqrt{3}y + 3 = 0$
• B. (i) $(a/b)^{1/3} x - y - a(b/a)^{1/3} = 0$, (ii) $y = 0$, (iii) $x - 2y - 1 = 0$, (iv) $x = 0$, $x + \sqrt{3}y - 3 = 0$, $x - \sqrt{3}y - 3 = 0$
• C. (i) $y = mx + a/m$ where $m^3 = -a/b$, (ii) $x = 0$, (iii) $x + 2y + 1 = 0$, (iv) $x = 0$, $x + \sqrt{3}y + 3 = 0$, $x - \sqrt{3}y + 3 = 0$
• D. (i) $(a/b)^{1/3} x + y - a(b/a)^{1/3} = 0$, (ii) $x = 0$, (iii) $x - 2y + 1 = 0$, (iv) $x = 0$, $x + \sqrt{3}y - 3 = 0$, $x - \sqrt{3}y - 3 = 0$

Answer 1

Answer: (A)

(i) $(a/b)^{1/3} x + y + a(b/a)^{1/3} = 0$, (ii) $x = 0$, (iii) $x + 2y - 1 = 0$, (iv) $x = 0$, $x - \sqrt{3}y + 3 = 0$, $x + \sqrt{3}y + 3 = 0$

Answer 2

(i) For parabolas $y^2=4ax$ and $x^2=4by$, the common tangent is found by equating the general tangent form $y=mx+a/m$ to the condition of tangency for the second parabola, leading to $m^3=-a/b$. The real root for $m$ gives the slope, and substituting back into $y=mx+a/m$ yields the tangent equation. The equation is $(a/b)^{1/3} x + y + a(b/a)^{1/3} = 0$. (ii) The circle $(x-2a)^2+y^2=(2a)^2$ and parabola $y^2=4ax$ intersect only at $(0,0)$. The tangent to the parabola at $(0,0)$ is $x=0$. The tangent to the circle at $(0,0)$ is also $x=0$. Thus, $x=0$ is the only common tangent. (iii) For parabolas $x^2=-8y$ and $y^2=-x$, we use the tangent form $y=mx-b/m$ for $y^2=-x$ (where $b=1/4$). Substituting into $x^2=-8y$ and setting the discriminant to zero gives $m^3=-b/2$. For $b=1/4$, $m=-1/2$. Substituting $m$ back into the tangent equation gives $x+2y-1=0$. (iv) The circle $(x-3)^2+y^2=9$ and parabola $y^2=4x$ intersect at $(0,0)$, $(2, 2\sqrt{2})$, and $(2, -2\sqrt{2})$. The tangent at $(0,0)$ for both is $x=0$. For other tangents, we use the general tangent to the parabola $y=mx+1/m$ and apply the condition that the distance from the circle's center $(3,0)$ to this line equals the radius $3$. This yields $m^2=1/3$, giving $m=\pm 1/\sqrt{3}$, and thus two more tangent lines: $x - \sqrt{3}y + 3 = 0$ and $x + \sqrt{3}y + 3 = 0$.