Question

Find area enclosed by $y = \frac{lnx}{ex}$.

Answer 1

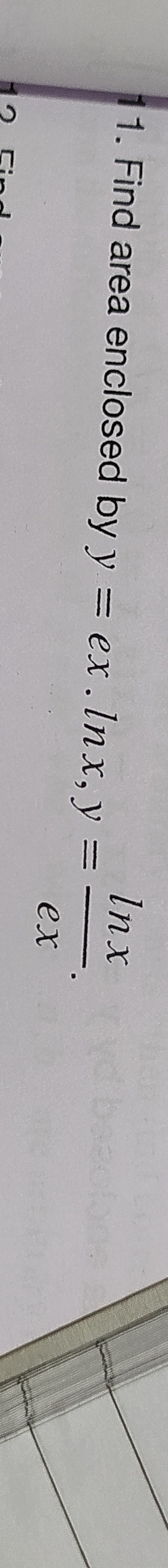
Infinite

Answer 2

To find the area enclosed by the curve $y = \frac{\ln x}{ex}$, we first analyze the function:

1. Domain: For $\ln x$ to be defined, $x > 0$.
2. x-intercept: Set $y=0$. $\frac{\ln x}{ex} = 0 \implies \ln x = 0 \implies x = e^0 = 1$. The curve intersects the x-axis at $x=1$.
3. Behavior as $x \to 0^+$: $\lim_{x \to 0^+} \frac{\ln x}{ex} = \frac{-\infty}{0^+} = -\infty$. The y-axis ($x=0$) is a vertical asymptote.
4. Behavior as $x \to \infty$: $\lim_{x \to \infty} \frac{\ln x}{ex}$. This is an indeterminate form $\frac{\infty}{\infty}$. Using L'Hopital's rule: $\lim_{x \to \infty} \frac{1/x}{e} = \lim_{x \to \infty} \frac{1}{ex} = 0$. The x-axis ($y=0$) is a horizontal asymptote.

Graph Sketch: The curve starts from $-\infty$ near the y-axis, crosses the x-axis at $x=1$, rises to a maximum (at $x=e$, $y=1/e^2$), and then approaches the x-axis as $x \to \infty$. For $0 < x < 1$, $\ln x < 0$, so $y < 0$ (the curve is below the x-axis). For $x > 1$, $\ln x > 0$, so $y > 0$ (the curve is above the x-axis).

Area Calculation: The "area enclosed by the curve" usually refers to the area between the curve and the x-axis. Since the curve extends to infinity and approaches the x-axis, this involves an improper integral. The total area $A$ is the sum of the absolute value of the integral from $0$ to $1$ and the integral from $1$ to $\infty$: $A = \int_{0}^{1} \left| \frac{\ln x}{ex} \right| dx + \int_{1}^{\infty} \frac{\ln x}{ex} dx$ Since $\frac{\ln x}{ex} < 0$ for $0 < x < 1$, the first integral becomes: $A = \int_{0}^{1} -\frac{\ln x}{ex} dx + \int_{1}^{\infty} \frac{\ln x}{ex} dx$

First, let's find the indefinite integral: $\int \frac{\ln x}{ex} dx = \frac{1}{e} \int \frac{\ln x}{x} dx$ Let $u = \ln x$, then $du = \frac{1}{x} dx$. $\frac{1}{e} \int u du = \frac{1}{e} \frac{u^2}{2} + C = \frac{(\ln x)^2}{2e} + C$.

Now, evaluate the definite integrals:

Part 1: Area from $x=0$ to $x=1$ $A_1 = \int_{0}^{1} -\frac{\ln x}{ex} dx = - \left[ \frac{(\ln x)^2}{2e} \right]_{0}^{1}$ $A_1 = - \left( \frac{(\ln 1)^2}{2e} - \lim_{a \to 0^+} \frac{(\ln a)^2}{2e} \right)$ Since $\ln 1 = 0$, this simplifies to: $A_1 = - \left( 0 - \lim_{a \to 0^+} \frac{(\ln a)^2}{2e} \right)$ As $a \to 0^+$, $\ln a \to -\infty$, so $(\ln a)^2 \to \infty$. Thus, $A_1 = - (0 - \infty) = \infty$.

Part 2: Area from $x=1$ to $x=\infty$ $A_2 = \int_{1}^{\infty} \frac{\ln x}{ex} dx = \left[ \frac{(\ln x)^2}{2e} \right]_{1}^{\infty}$ $A_2 = \lim_{b \to \infty} \frac{(\ln b)^2}{2e} - \frac{(\ln 1)^2}{2e}$ Since $\ln 1 = 0$, this simplifies to: $A_2 = \lim_{b \to \infty} \frac{(\ln b)^2}{2e} - 0$ As $b \to \infty$, $\ln b \to \infty$, so $(\ln b)^2 \to \infty$. Thus, $A_2 = \infty$.

Since both parts of the area calculation result in infinity, the total area enclosed by the curve and the x-axis is infinite.

Conclusion: The area enclosed by the curve $y = \frac{\ln x}{ex}$ is infinite. In mathematical terms, the improper integral diverges.

Explanation of the solution: The area enclosed by the curve $y = \frac{\ln x}{ex}$ and the x-axis is given by the improper integral $\int_0^\infty \left| \frac{\ln x}{ex} \right| dx$. This integral is split into two parts: $\int_0^1 -\frac{\ln x}{ex} dx$ and $\int_1^\infty \frac{\ln x}{ex} dx$. The indefinite integral of $\frac{\ln x}{ex}$ is $\frac{(\ln x)^2}{2e}$. Evaluating the first part, $\lim_{a \to 0^+} -\left[\frac{(\ln x)^2}{2e}\right]_a^1 = \infty$. Evaluating the second part, $\lim_{b \to \infty} \left[\frac{(\ln x)^2}{2e}\right]_1^b = \infty$. Since both parts diverge to infinity, the total area is infinite.