Question

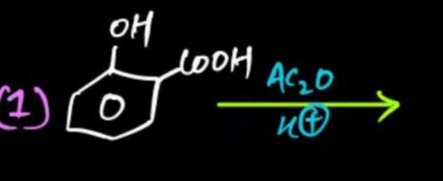
(1) $\xrightarrow{\substack{Ac_2O \\ H^+}}$

Answer 1

The product of the reaction is Acetylsalicylic acid (Aspirin). The structure is: O=C(O)c1ccccc1OC(=O)C

Answer 2

The given reactant is salicylic acid (2-hydroxybenzoic acid). The reagents are acetic anhydride ($Ac_2O$) and an acid catalyst ($H^+$).

This is an acylation reaction. Salicylic acid contains two functional groups: a phenolic hydroxyl group (-OH) and a carboxylic acid group (-COOH). Acetic anhydride is an acylating agent that reacts with hydroxyl groups (alcohols and phenols) to form esters.

Among the two functional groups in salicylic acid, the phenolic -OH group is more reactive towards acylation by acetic anhydride in the presence of an acid catalyst. The carboxylic acid group generally does not react under these conditions to form an ester or a mixed anhydride as the primary product.

The phenolic -OH group of salicylic acid undergoes esterification with acetic anhydride. The acetyl group ($CH_3CO-$) from acetic anhydride is transferred to the phenolic oxygen, forming an ester linkage. Acetic acid ($CH_3COOH$) is produced as a byproduct.

The reaction can be represented as: Salicylic acid + Acetic anhydride $\xrightarrow{H^+}$ Acetylsalicylic acid + Acetic acid

The product formed is 2-acetoxybenzoic acid, commonly known as Aspirin.

Reaction:

\begin{center}
\begin{tikzpicture}[scale=0.8]
    % Salicylic acid
    \node (benzene) at (0,0) {\text{}};
    \draw (benzene) ++(-1,0) -- ++(-0.5,0.866) -- ++(0.5,0.866) -- ++(1,0) -- ++(0.5,-0.866) -- ++(-0.5,-0.866) -- cycle;
    \draw (benzene) ++(0,0.866) -- ++(0.866,0) -- ++(0,-0.866) -- ++(-0.866,0) -- cycle; % Inner circle approximation
    \node at (0,0) {\text{}}; % Dot for inner circle
    \node at (1.5, 1.7) {\text{OH}};
    \draw (1.2, 1.2) -- (1.5, 1.7); % OH bond
    \node at (2.4, 0.5) {\text{COOH}};
    \draw (1.5, 0.866) -- (2.4, 0.5); % COOH bond
    \node at (0.5, 2.5) {\text{Salicylic acid}};

    % Acetic anhydride
    \node at (4, 0.8) {\text{$+$}};
    \node at (5.5, 0.8) {\text{$(CH_3CO)_2O$}};
    \node at (5.5, 0.2) {\text{Acetic anhydride}};

    % Arrow with reagents
    \draw[->, thick, green] (7, 0.8) -- (9, 0.8);
    \node at (8, 1.3) {\text{$Ac_2O$}};
    \node at (8, 0.3) {\text{$H^+$}};

    % Acetylsalicylic acid (Aspirin)
    \node (product_benzene) at (11,0) {\text{}};
    \draw (product_benzene) ++(-1,0) -- ++(-0.5,0.866) -- ++(0.5,0.866) -- ++(1,0) -- ++(0.5,-0.866) -- ++(-0.5,-0.866) -- cycle;
    \draw (product_benzene) ++(0,0.866) -- ++(0.866,0) -- ++(0,-0.866) -- ++(-0.866,0) -- cycle; % Inner circle approximation
    \node at (11,0) {\text{}}; % Dot for inner circle
    \node at (12.5, 1.7) {\text{OCOCH$_3$}};
    \draw (12.2, 1.2) -- (12.5, 1.7); % OCOCH3 bond
    \node at (13.4, 0.5) {\text{COOH}};
    \draw (12.5, 0.866) -- (13.4, 0.5); % COOH bond
    \node at (11.5, 2.5) {\text{Acetylsalicylic acid (Aspirin)}};
\end{tikzpicture}
\end{center}

The product is 2-acetoxybenzoic acid.

Explanation of the solution:

Salicylic acid reacts with acetic anhydride in the presence of an acid catalyst. The phenolic -OH group of salicylic acid is acetylated by acetic anhydride, forming an ester. The carboxylic acid group remains unaffected. The product is acetylsalicylic acid (Aspirin).