Question

Figure shows a potentiometer circuit. The length of potentiometer wire AB is 120 cm and its resistance is $2\Omega$. The internal resistance of 2V cell is $1\Omega$. Initially the switches $S_1$ and $S_2$ are open and $S_3$ is closed.

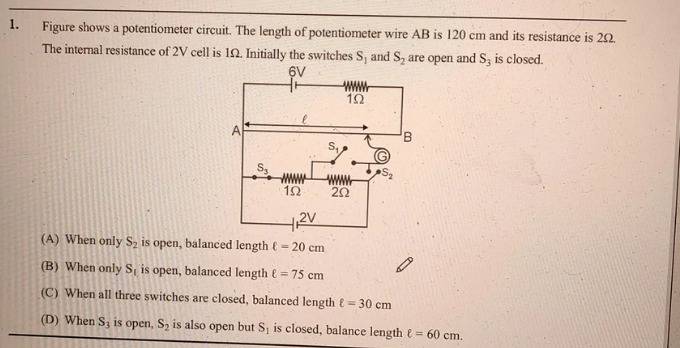
• A. When only $S_2$ is open, balanced length $\ell$ = 20 cm
• B. When only $S_1$ is open, balanced length $\ell$ = 75 cm
• C. When all three switches are closed, balanced length $\ell$ = 30 cm
• D. When $S_3$ is open, $S_2$ is also open but $S_1$ is closed, balance length $\ell$ = 60 cm.

Answer 1

Answer: (C)

C

Answer 2

The potential gradient along the potentiometer wire AB is $k = \frac{V_{AB}}{L_{AB}}$.

The total resistance of the primary circuit is $R_{total} = R_{AB} + R_{ext} = 2\Omega + 1\Omega = 3\Omega$.

The current in the primary circuit is $I_p = \frac{EMF_{primary}}{R_{total}} = \frac{6V}{3\Omega} = 2A$.

The potential difference across the potentiometer wire AB is $V_{AB} = I_p \times R_{AB} = 2A \times 2\Omega = 4V$.

The potential gradient is $k = \frac{4V}{120 cm} = \frac{1}{30} V/cm$.

(A) When only $S_2$ is open, $S_1$ and $S_3$ are closed. The galvanometer is connected to the junction between the $1\Omega$ and $2\Omega$ resistors. Point A is connected to the negative terminal of the 2V cell. The positive terminal of the 2V cell is connected to the series combination of the internal resistance ($1\Omega$) and the $1\Omega$ resistor (since $S_3$ is closed). This series combination is connected to the junction between the $1\Omega$ and $2\Omega$ resistors. The potential difference between A and the junction is the potential difference across the 2V cell and the $1\Omega$ internal resistance and the $1\Omega$ external resistor. The current in the secondary circuit is $I_s = \frac{2V}{1\Omega + 1\Omega + 2\Omega} = \frac{2}{4} = 0.5A$.

The potential difference between A (negative terminal) and the junction between $1\Omega$ and $2\Omega$ is $V_{AJ} = V_{cell} - I_s(r + R_3) = 2V - 0.5A(1\Omega + 1\Omega) = 2V - 0.5A \times 2\Omega = 2V - 1V = 1V$.

Balanced length $\ell = \frac{V_{AJ}}{k} = \frac{1V}{1/30 V/cm} = 30 cm$. Option (A) is incorrect.

(B) When only $S_1$ is open, $S_2$ and $S_3$ are closed. The galvanometer is connected to the point after the $2\Omega$ resistor. This point is the positive terminal of the 2V cell. Point A is the negative terminal. The potential difference to be balanced is the terminal voltage of the 2V cell. The current in the secondary circuit is $I_s = \frac{2V}{1\Omega + 1\Omega + 2\Omega} = 0.5A$. The terminal voltage is $V_t = EMF - I_s r = 2V - 0.5A \times 1\Omega = 2V - 0.5V = 1.5V$.

Balanced length $\ell = \frac{V_t}{k} = \frac{1.5V}{1/30 V/cm} = 1.5 \times 30 cm = 45 cm$. Option (B) is incorrect.

(C) When all three switches are closed, $S_1, S_2, S_3$ are closed. The galvanometer is connected between the jockey and the junction between the $1\Omega$ and $2\Omega$ resistors. Point A is connected to the negative terminal of the 2V cell. The positive terminal of the 2V cell is connected to the series combination of the internal resistance ($1\Omega$) and the $1\Omega$ resistor (since $S_3$ is closed). This series combination is connected to the junction between the $1\Omega$ and $2\Omega$ resistors. This is the same configuration as in (A).

Potential difference to be balanced is $1V$. Balanced length $\ell = \frac{1V}{1/30 V/cm} = 30 cm$. Option (C) is correct.

(D) When $S_3$ is open, $S_2$ is also open but $S_1$ is closed. $S_3$ and $S_2$ are open, $S_1$ is closed. The galvanometer is connected to the junction between the $1\Omega$ and $2\Omega$ resistors. Since $S_3$ is open, the $1\Omega$ resistor in series with $S_3$ is not in the circuit. The secondary circuit consists of the 2V cell with internal resistance $1\Omega$ and the $2\Omega$ resistor. The galvanometer is connected to the junction between the cell and the $2\Omega$ resistor. Point A is connected to the negative terminal of the 2V cell. The galvanometer is connected to the positive terminal of the 2V cell.

The potential difference to be balanced is the terminal voltage of the 2V cell. The current in the secondary circuit is $I_s = \frac{2V}{1\Omega + 2\Omega} = \frac{2}{3}A$. The terminal voltage is $V_t = EMF - I_s r = 2V - \frac{2}{3}A \times 1\Omega = 2V - \frac{2}{3}V = \frac{4}{3}V$.

Balanced length $\ell = \frac{V_t}{k} = \frac{4/3 V}{1/30 V/cm} = \frac{4}{3} \times 30 cm = 4 \times 10 cm = 40 cm$. Option (D) is incorrect.