Question

Evaluate the integral $\int_{-1}^{1}\int_{0}^{\pi/2} x \sin \sqrt{y} \,dy\,dx$

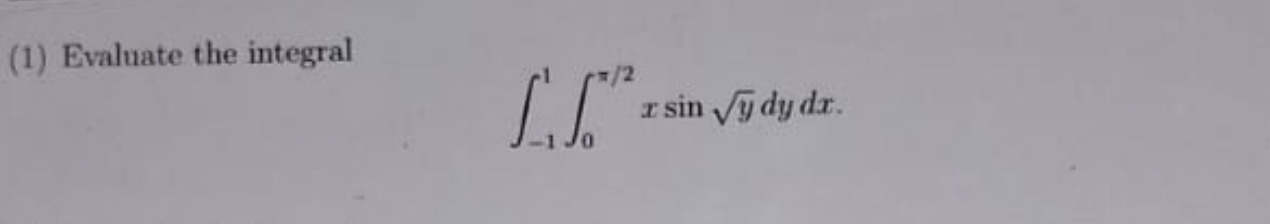
Answer 1

0

Answer 2

The integral can be separated into two independent integrals: $\left(\int_{-1}^{1} x \,dx\right) \left(\int_{0}^{\pi/2} \sin \sqrt{y} \,dy\right)$ The first integral, $\int_{-1}^{1} x \,dx$, evaluates to 0 because $x$ is an odd function integrated over a symmetric interval $[-1, 1]$. Since one of the factors is 0, the entire double integral is 0.