Question

1 + \cos 20^\circ + \cos 30^\circ + \cos 50^\circ =

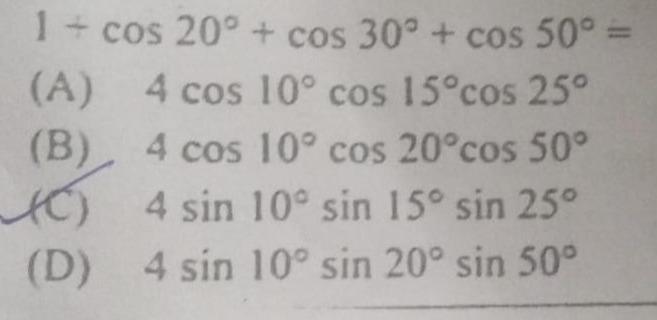
• A. 4 \cos 10^\circ \cos 15^\circ \cos 25^\circ
• B. 4 \cos 10^\circ \cos 20^\circ \cos 50^\circ
• C. 4 \sin 10^\circ \sin 15^\circ \sin 25^\circ
• D. 4 \sin 10^\circ \sin 20^\circ \sin 50^\circ

Answer 1

Answer: (A)

4 \cos 10^\circ \cos 15^\circ \cos 25^\circ

Answer 2

Here's how to solve the problem:

1. Rewrite using double-angle identity:

   $1 + \cos20^\circ = 2\cos^2 10^\circ$

2. Apply sum-to-product identity:

   $\cos30^\circ + \cos50^\circ = 2\cos\left(\frac{30^\circ+50^\circ}{2}\right)\cos\left(\frac{30^\circ-50^\circ}{2}\right) = 2\cos40^\circ \cos10^\circ$

3. Combine the terms:

   $2\cos^2 10^\circ + 2\cos40^\circ\cos10^\circ = 2\cos10^\circ\left(\cos10^\circ+\cos40^\circ\right)$

4. Apply sum-to-product identity again:

   $\cos10^\circ+\cos40^\circ = 2\cos\left(\frac{10^\circ+40^\circ}{2}\right)\cos\left(\frac{10^\circ-40^\circ}{2}\right) = 2\cos25^\circ \cos15^\circ$

5. Substitute back to get the final expression:

   $2\cos10^\circ \times 2\cos25^\circ\cos15^\circ = 4\cos10^\circ\cos15^\circ\cos25^\circ$

Therefore, the answer is $4\cos10^\circ\cos15^\circ\cos25^\circ$.