Question

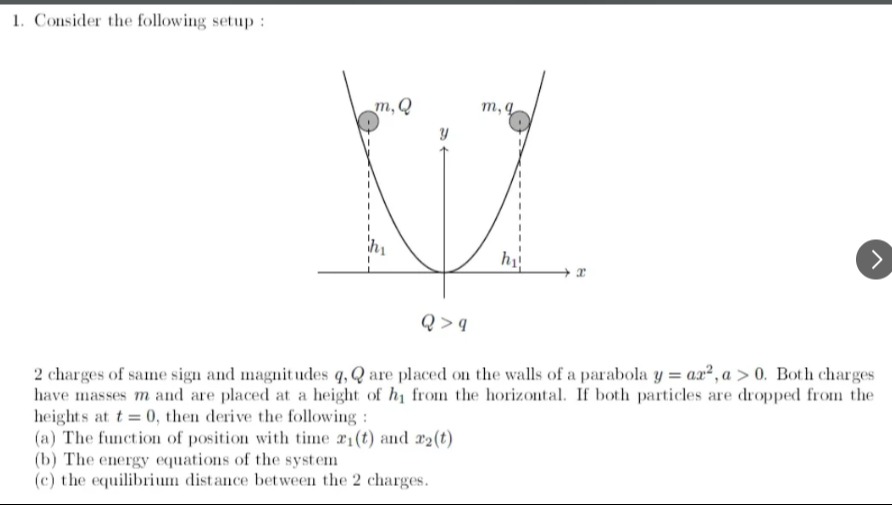
Consider the following setup:

2 charges of same sign and magnitudes $q, Q$ are placed on the walls of a parabola $y = ax^2, a > 0$. Both charges have masses $m$ and are placed at a height of $h_1$ from the horizontal. If both particles are dropped from the heights at $t = 0$, then derive the following:

(a) The function of position with time $x_1(t)$ and $x_2(t)$ (b) The energy equations of the system (c) the equilibrium distance between the 2 charges.

Answer 1

(a) $x_1(t)=-x(t)$ and $x_2(t)=x(t)$ with

$$m\Bigl[(1+4a^2x^2)\ddot x+4a^2x\,\dot x^2\Bigr] = -2mga\,x+\frac{kQq}{2x^2},\quad x(0)=\sqrt{h_1/a},\; \dot x(0)=0.$$

(b) Total energy

$$E = \frac{1}{2}m\Bigl[(1+4a^2x_1^2)\dot x_1^2+(1+4a^2x_2^2)\dot x_2^2\Bigr] + mga\,(x_1^2+x_2^2)+\frac{kQq}{|x_2-x_1|}.$$

For symmetry,

$$E= m\left[\frac{1}{2}(1+4a^2x^2)\dot x^2+ga\,x^2\right]+\frac{kQq}{2x}.$$

(c) Equilibrium when

$$8mga\,x_0^3 = kQq\quad\Longrightarrow\quad x_0=\left(\frac{kQq}{8mga}\right)^{1/3},\quad d_{eq}=2x_0.$$

Answer 2

Overview:

This problem involves analyzing the motion of two charged particles constrained to move along a parabolic path under the influence of gravity and electrostatic repulsion. The solution involves:

1. Parameterizing the motion along $y=ax^2$ so that kinetic energy becomes $\frac{1}{2}m(1+4a^2x^2)\dot x^2$.
2. Writing the potential energies: gravitational $mga\,x^2$ for each and Coulomb $kQq/(2x)$ (since $d=2x$).
3. Using Lagrange’s equations (or energy conservation) one obtains the differential equation for $x(t)$; hence the positions $x_1(t)=-x(t)$ and $x_2(t)=x(t)$.
4. Minimizing the potential energy $U(x)=2mga\,x^2+\frac{kQq}{2x}$ with respect to $x$ yields the equilibrium position $x_0=(kQq/(8mga))^{1/3}$ and so the equilibrium distance is $d_{eq}=2x_0$.

Detailed Steps:

Equations of Motion:

Because each particle is constrained to lie on the parabola $y=ax^2$ the arc‐length is

$$s(x)=\int_0^x\sqrt{1+(y')^2}\,dx=\int_0^x\sqrt{1+(2ax)^2}\,dx=\int_0^x\sqrt{1+4a^2x^2}\,dx.$$

Thus the velocity is

$$v=\frac{ds}{dt}=\sqrt{1+4a^2x^2}\,\dot x.$$

Hence the kinetic energy for a particle is

$$K=\frac{1}{2}m\Bigl(1+4a^2x^2\Bigr)\dot x^2.$$

Now, for the two particles (we label the left one “$(m,Q)$” and the right one “$(m,q)$” with $Q>q$) the energy contributions are:

1. Gravitational potential energy (using $y=ax^2$) for each is $$U_g=mga x^2.$$
2. Their mutual Coulomb potential energy is $$U_e=\frac{k\,Qq}{d},$$ where the distance between them is, when symmetric, $$d= \sqrt{(x_2-x_1)^2 + \Bigl(a(x_2^2-x_1^2)\Bigr)^2}.$$ But for $x_1=-x,x_2=x$ we have $x_2-x_1=2x$ and $$x_2^2-x_1^2=x^2-x^2=0,$$ so that $$d=2|x|.$$

Thus the Coulomb energy is

$$U_e=\frac{kQq}{2|x|}.$$

A Lagrange–Newton treatment along the $x$–coordinate leads to the equation of motion

$$m\frac{d}{dt}\Bigl[\sqrt{1+4a^2x^2}\,\dot x\Bigr] = -\frac{d}{dx}\Bigl[mga\,x^2+\frac{kQq}{2|x|}\Bigr].$$

In explicit form one may write

$$m\Bigl[(1+4a^2x^2)\ddot x+4a^2x\,\dot x^2\Bigr] = -2mga\,x+\frac{kQq}{2x^2},$$

where (for $x>0$) we have dropped the absolute value. Then the positions of the two charges are

$$x_1(t)=-x(t),\qquad x_2(t)=x(t),$$

with the above differential equation governing $x(t)$. (One may “solve” for $t$ in terms of $x$ by writing

$$t = \int_{x(0)}^{x(t)} \frac{\sqrt{1+4a^2x^2}}{\sqrt{\frac{2}{m}\Bigl[\,mga\,(x(0)^2-x^2)+\frac{kQq}{2}\Bigl(\frac{1}{x} -\frac{1}{x(0)}\Bigr)\Bigr]}}\,dx,$$

where $x(0)=\sqrt{h_1/a}$, the initial position along $x$, since the particles are dropped from a height $h_1$ above $x$-axis.)

Energy equations

The total energy of the two–particle system is conserved. For each particle the energy is

• Kinetic: $$K_i=\frac{1}{2}m\Bigl(1+4a^2x_i^2\Bigr)\dot x_i^2,$$
• Gravitational potential: $$U_{g,i}=mga\,x_i^2.$$

Thus, if we write the energies for the two and add the Coulomb interaction, the conserved energy reads

$$E = \frac{1}{2}m\Bigl[(1+4a^2x_1^2)\dot x_1^2+(1+4a^2x_2^2)\dot x_2^2\Bigr] + mga\,(x_1^2+x_2^2)+\frac{kQq}{|x_2-x_1|}.$$

For the symmetric case $x_1=-x$ and $x_2=x$ this becomes

$$E = m\left[\frac{1}{2}\Bigl(1+4a^2x^2\Bigr)\dot x^2 +ga\, x^2\right] +\frac{kQq}{2|x|}\,.$$

Equilibrium distance

In equilibrium the forces along the tangent vanish. Equivalently the energy is minimized with respect to $x$. For the symmetric case, the potential energy (of the system) is

$$U(x)=2mga\,x^2+\frac{kQq}{2x}\quad (x>0).$$

Setting $\frac{dU}{dx}=0$ we get

$$\frac{dU}{dx} = 4mga\,x - \frac{kQq}{2x^2}=0.$$

Thus,

$$4mga\,x = \frac{kQq}{2x^2}\quad\Longrightarrow\quad 8mga\,x^3=kQq.$$

Therefore,

$$x_0=\Bigl(\frac{kQq}{8mga}\Bigr)^{\!1/3}.$$

Since the charges are separated by a horizontal distance of $2x$, the equilibrium distance is

$$d_{eq}=2x_0=2\Bigl(\frac{kQq}{8mga}\Bigr)^{\!1/3}\,.$$