Question

Consider the following heat engine involving one mole of ideal monatomic gas. The gas begins at temperature $T_0$, pressure $P_0$, and volume $V_0$, and undergoes four reversible steps.

1. The gas is expanded at constant pressure until its

Answer 1

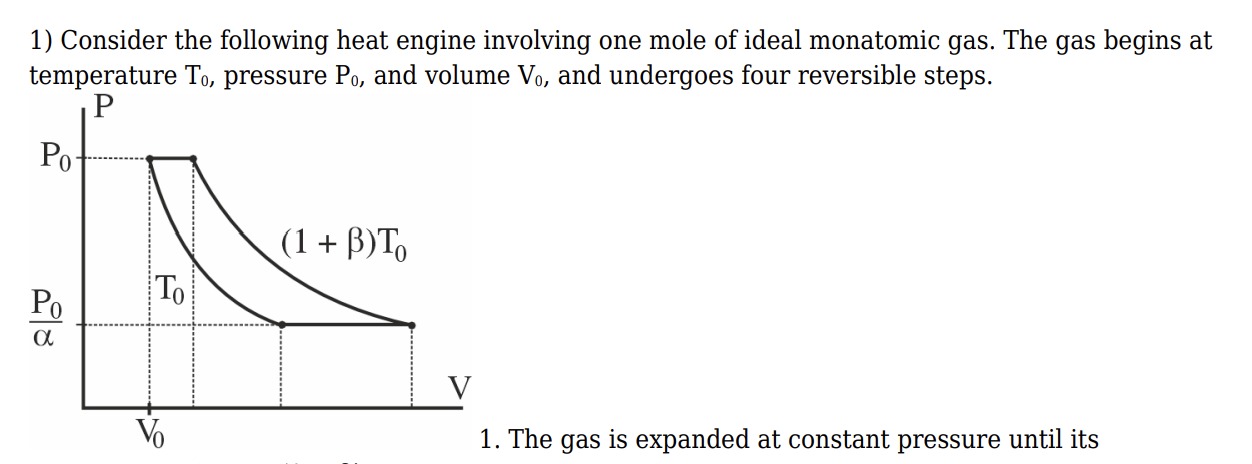
temperature is (1+\beta)T_0

Answer 2

The provided question is incomplete. It asks to complete the sentence describing the first step of the heat engine cycle. Based on the diagram and the description of the initial state and the nature of the first step, the first step is a constant pressure expansion from state 1 to state 2.

State 1: $(P_0, V_0, T_0)$.

The first step is at constant pressure $P_0$. From the diagram, the process goes from temperature $T_0$ to $(1+\beta)T_0$.

Using the ideal gas law $PV = nRT$, with $n=1$, we have $P_0 V_0 = RT_0$.

Let state 2 be $(P_2, V_2, T_2)$. For the first step, $P_2 = P_0$ and $T_2 = (1+\beta)T_0$.

From the ideal gas law at state 2, $P_2 V_2 = RT_2$, so $P_0 V_2 = R(1+\beta)T_0$.

Dividing by $P_0 V_0 = RT_0$, we get $\frac{V_2}{V_0} = \frac{(1+\beta)T_0}{T_0} = 1+\beta$.

So, $V_2 = (1+\beta)V_0$.

The first step is a constant pressure expansion from $(P_0, V_0, T_0)$ to $(P_0, (1+\beta)V_0, (1+\beta)T_0)$.

The sentence "1. The gas is expanded at constant pressure until its" can be completed by stating either the final volume or the final temperature.

Possible completions are:

• volume is $(1+\beta)V_0$.

• temperature is $(1+\beta)T_0$.

Since the options are not given, we cannot select the correct option. However, if the question asks for the description of the first step, either of the above completions would be appropriate. Assuming a multiple choice question, one of these would likely be an option.