Question

Circles of radii 5, 5 and 8 are mutually externally tangent. If a fourth circle of radius r touches all the three circles externally, then the value of r is

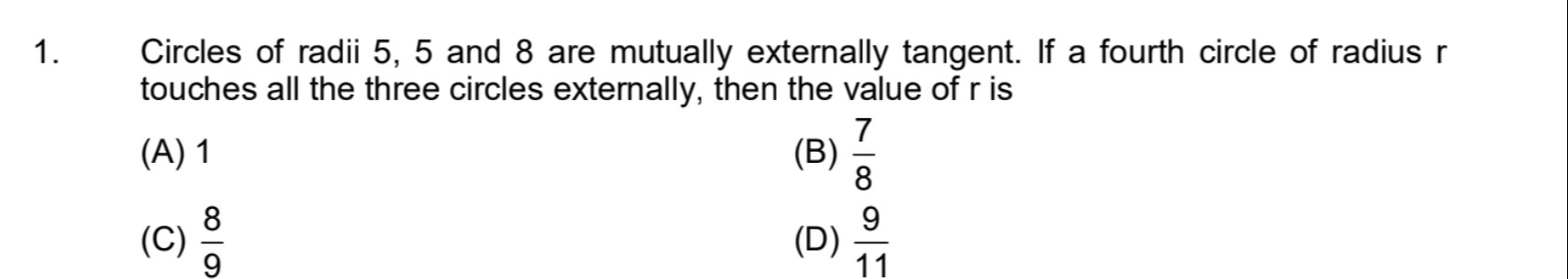
• A. 1
• B. $\frac{7}{8}$
• C. $\frac{8}{9}$
• D. $\frac{9}{11}$

Answer 1

Answer: (C)

$\frac{8}{9}$

Answer 2

The problem asks for the radius of a fourth circle that touches three given mutually externally tangent circles. The radii of the three given circles are $R_1=5$, $R_2=5$, and $R_3=8$. Let the radius of the fourth circle be $r$.

This problem can be solved using Descartes' Theorem, which relates the curvatures of four mutually tangent circles. The curvature $k$ of a circle is defined as $1/R$, where $R$ is its radius. For four mutually tangent circles, if they are all externally tangent, or if one circle encloses the other three, Descartes' Theorem states:

$(k_1 + k_2 + k_3 + k_4)^2 = 2(k_1^2 + k_2^2 + k_3^2 + k_4^2)$

In this problem, all circles are externally tangent, so all curvatures are positive. The curvatures of the three given circles are:

$k_1 = \frac{1}{R_1} = \frac{1}{5}$

$k_2 = \frac{1}{R_2} = \frac{1}{5}$

$k_3 = \frac{1}{R_3} = \frac{1}{8}$

Let the curvature of the fourth circle be $k_4 = \frac{1}{r}$.

Substitute these values into Descartes' Theorem:

$\left(\frac{1}{5} + \frac{1}{5} + \frac{1}{8} + \frac{1}{r}\right)^2 = 2\left(\left(\frac{1}{5}\right)^2 + \left(\frac{1}{5}\right)^2 + \left(\frac{1}{8}\right)^2 + \left(\frac{1}{r}\right)^2\right)$

Simplify the terms:

$\left(\frac{2}{5} + \frac{1}{8} + \frac{1}{r}\right)^2 = 2\left(\frac{1}{25} + \frac{1}{25} + \frac{1}{64} + \frac{1}{r^2}\right)$

$\left(\frac{16+5}{40} + \frac{1}{r}\right)^2 = 2\left(\frac{2}{25} + \frac{1}{64} + \frac{1}{r^2}\right)$

$\left(\frac{21}{40} + \frac{1}{r}\right)^2 = 2\left(\frac{128+25}{1600} + \frac{1}{r^2}\right)$

$\left(\frac{21}{40} + \frac{1}{r}\right)^2 = 2\left(\frac{153}{1600} + \frac{1}{r^2}\right)$

Expand the left side:

$\left(\frac{21}{40}\right)^2 + 2\left(\frac{21}{40}\right)\left(\frac{1}{r}\right) + \left(\frac{1}{r}\right)^2 = \frac{306}{1600} + \frac{2}{r^2}$

$\frac{441}{1600} + \frac{42}{40r} + \frac{1}{r^2} = \frac{306}{1600} + \frac{2}{r^2}$

$\frac{441}{1600} + \frac{21}{20r} + \frac{1}{r^2} = \frac{306}{1600} + \frac{2}{r^2}$

Rearrange the terms to form a quadratic equation in $\frac{1}{r}$:

$0 = \left(\frac{2}{r^2} - \frac{1}{r^2}\right) - \frac{21}{20r} + \left(\frac{306}{1600} - \frac{441}{1600}\right)$

$0 = \frac{1}{r^2} - \frac{21}{20r} - \frac{135}{1600}$

$0 = \frac{1}{r^2} - \frac{21}{20r} - \frac{27}{320}$ (dividing 135 and 1600 by 5)

Let $x = \frac{1}{r}$. The equation becomes:

$x^2 - \frac{21}{20}x - \frac{27}{320} = 0$

Multiply the entire equation by 320 to eliminate denominators:

$320x^2 - 320\left(\frac{21}{20}\right)x - 320\left(\frac{27}{320}\right) = 0$

$320x^2 - 16 \times 21x - 27 = 0$

$320x^2 - 336x - 27 = 0$

Use the quadratic formula $x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$:

$x = \frac{336 \pm \sqrt{(-336)^2 - 4(320)(-27)}}{2(320)}$

$x = \frac{336 \pm \sqrt{112896 + 34560}}{640}$

$x = \frac{336 \pm \sqrt{147456}}{640}$

Calculate the square root: $\sqrt{147456} = 384$.

$x = \frac{336 \pm 384}{640}$

Two possible values for $x$:

1. $x_1 = \frac{336 + 384}{640} = \frac{720}{640} = \frac{72}{64} = \frac{9}{8}$

2. $x_2 = \frac{336 - 384}{640} = \frac{-48}{640} = -\frac{3}{40}$

Since the fourth circle touches the three circles externally, its radius $r$ must be positive. Therefore, its curvature $x = 1/r$ must also be positive.

So, we choose $x = \frac{9}{8}$.

Since $x = \frac{1}{r}$, we have $\frac{1}{r} = \frac{9}{8}$.

Therefore, $r = \frac{8}{9}$.

The other solution $x_2 = -3/40$ corresponds to $r = -40/3$. A negative radius in Descartes' Theorem indicates that the circle encloses the other three circles. However, the problem specifies "touches all the three circles externally", so we take the positive radius solution.