Question

Calculate the potential of Iron electrode in which the concentration of Fe2+ ion is 0.01 M. (2024)

(E°Fe2+/Fe = 0.45 V at 298 K)

[Given: log 10 = 1]

Answer 1

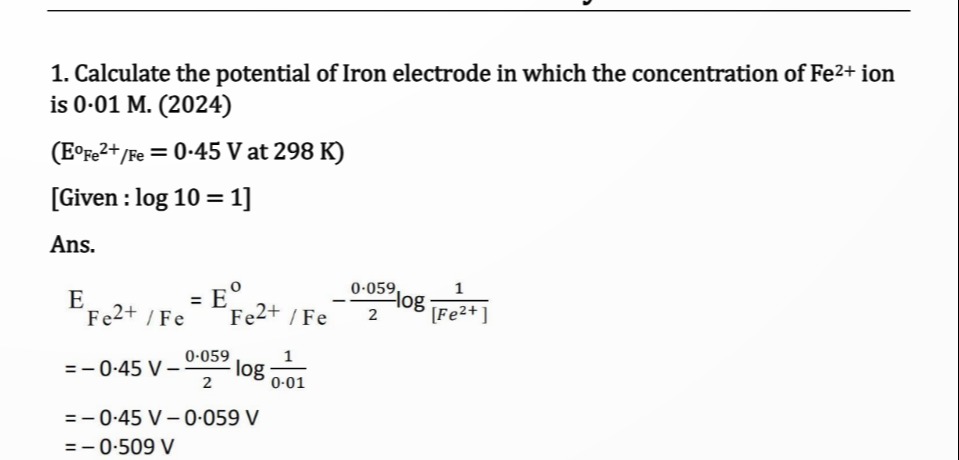
EFe2+ / Fe = -0.509 V

Answer 2

The problem requires calculating the electrode potential of an Iron electrode under non-standard conditions using the Nernst equation.

1. Identify the half-reaction and number of electrons (n): The reduction half-reaction for the iron electrode is: $\text{Fe}^{2+}(aq) + 2e^- \rightarrow \text{Fe}(s)$ From this, the number of electrons involved, $n = 2$.

2. Identify the given values:

• Concentration of Fe²⁺, $[\text{Fe}^{2+}] = 0.01 \text{ M}$
• Standard electrode potential, $E^\circ_{\text{Fe}^{2+}/\text{Fe}} = 0.45 \text{ V}$ (as stated in the question). However, the provided solution uses $-0.45 \text{ V}$. Standard reduction potential for $\text{Fe}^{2+}/\text{Fe}$ is typically negative (around $-0.44 \text{ V}$ to $-0.45 \text{ V}$). Given that the provided solution proceeds with $-0.45 \text{ V}$ and arrives at a chemically plausible result, we will assume $E^\circ_{\text{Fe}^{2+}/\text{Fe}} = -0.45 \text{ V}$ for consistency with the provided solution's calculation.
• Temperature, $T = 298 \text{ K}$ (implied by the use of 0.059 in the Nernst equation).
• Given: $\log 10 = 1$.

3. Apply the Nernst equation: The Nernst equation for a reduction half-reaction $M^{n+}(aq) + ne^- \rightarrow M(s)$ at 298 K is: $E_{M^{n+}/M} = E^\circ_{M^{n+}/M} - \frac{0.059}{n} \log \frac{1}{[M^{n+}]}$

Substitute the values for the Iron electrode: $E_{\text{Fe}^{2+}/\text{Fe}} = E^\circ_{\text{Fe}^{2+}/\text{Fe}} - \frac{0.059}{2} \log \frac{1}{[\text{Fe}^{2+}]}$ $E_{\text{Fe}^{2+}/\text{Fe}} = -0.45 \text{ V} - \frac{0.059}{2} \log \frac{1}{0.01}$

4. Calculate the logarithmic term: $\log \frac{1}{0.01} = \log \frac{1}{\frac{1}{100}} = \log 100$ Since $100 = 10^2$, we have: $\log 100 = \log (10^2) = 2 \log 10$ Given $\log 10 = 1$, $\log 100 = 2 \times 1 = 2$

5. Complete the calculation: Substitute the value of the logarithmic term back into the Nernst equation: $E_{\text{Fe}^{2+}/\text{Fe}} = -0.45 \text{ V} - \frac{0.059}{2} \times 2$ $E_{\text{Fe}^{2+}/\text{Fe}} = -0.45 \text{ V} - 0.059 \text{ V}$ $E_{\text{Fe}^{2+}/\text{Fe}} = -0.509 \text{ V}$

The calculated potential of the Iron electrode is $-0.509 \text{ V}$.

Explanation of the solution:

The electrode potential for the Iron electrode is calculated using the Nernst equation.

1. Reaction: $\text{Fe}^{2+}(aq) + 2e^- \rightarrow \text{Fe}(s)$. Here, $n=2$.
2. Nernst Equation: $E = E^\circ - \frac{0.059}{n} \log \frac{1}{[\text{Fe}^{2+}]}$ at 298 K.
3. Substitute values: $E^\circ = -0.45 \text{ V}$ (assuming this value, consistent with the provided solution's calculation), $n=2$, $[\text{Fe}^{2+}] = 0.01 \text{ M}$. $E = -0.45 - \frac{0.059}{2} \log \frac{1}{0.01}$
4. Calculate log term: $\log \frac{1}{0.01} = \log 100 = 2$.
5. Final Calculation: $E = -0.45 - \frac{0.059}{2} \times 2 = -0.45 - 0.059 = -0.509 \text{ V}$.

Answer:

The potential of the Iron electrode is -0.509 V.