Question

As shown a smooth hemisphere, of mass $M = 4$ kg and radius $a = 2$ m, is placed with its plane base on a smooth table. A rod, of mass $m = 2$ kg is constrained to move in a vertical line with one end $P$ on the curved surface of the hemisphere. Find the angular speed (in rad/s) of point $P$ with respect to centre $O$ of the hemisphere when $OP$ makes an angle $\theta = 60°$ with the vertical. Initially the rod was at the topmost point of the hemisphere. ($g = 10 \ m/s^2$)

Answer 1

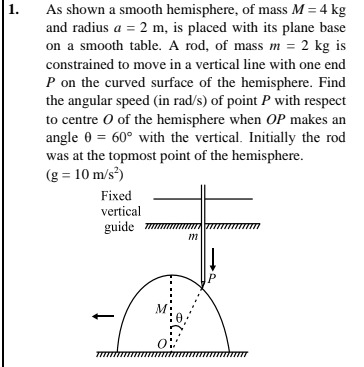
2

Answer 2

The problem involves a system of a hemisphere and a rod, both of which can move. Since all surfaces are smooth, there is no friction, implying that mechanical energy is conserved. The rod is constrained to move vertically by a fixed guide, and the hemisphere is on a smooth horizontal table.

1. Conservation of Mechanical Energy: The system consists of the rod (mass $m$) and the hemisphere (mass $M$).

• Initial State: The rod is at the topmost point of the hemisphere. Both are at rest.
  Let the potential energy reference be the base of the hemisphere.
  Initial height of point P (on the rod) is $a$.
  Initial Kinetic Energy, $KE_i = 0$.
  Initial Potential Energy, $PE_i = mga$.
  Total Initial Energy, $E_i = mga$.

• Final State: OP makes an angle $\theta = 60°$ with the vertical.
  Let $v_M$ be the horizontal velocity of the hemisphere and $v_m$ be the vertical velocity of the rod.
  Final Kinetic Energy, $KE_f = \frac{1}{2} M v_M^2 + \frac{1}{2} m v_m^2$.
  Final height of point P is $a \cos\theta$.
  Final Potential Energy, $PE_f = mg a \cos\theta$.
  Total Final Energy, $E_f = \frac{1}{2} M v_M^2 + \frac{1}{2} m v_m^2 + mg a \cos\theta$.

By conservation of mechanical energy ($E_i = E_f$): $mga = \frac{1}{2} M v_M^2 + \frac{1}{2} m v_m^2 + mg a \cos\theta$
$\frac{1}{2} M v_M^2 + \frac{1}{2} m v_m^2 = mga(1 - \cos\theta)$ (Equation 1)

2. Kinematic Constraint (Relation between $v_M$ and $v_m$): Point P is always on the surface of the hemisphere.
Let the position of the center of the hemisphere be $(X, 0)$ and the rod be constrained to move along the vertical line $x_P = x_0$.
The equation of the hemisphere surface for point P at $(x_P, y_P)$ is $(x_P - X)^2 + y_P^2 = a^2$.
Differentiating this equation with respect to time:
$2(x_P - X)(\dot{x}_P - \dot{X}) + 2y_P \dot{y}_P = 0$.
We know $\dot{x}_P = 0$ (rod moves vertically).
Let $\dot{X} = v_M$ (velocity of hemisphere).
Let $\dot{y}_P = v_m$ (velocity of rod).
So, $(x_P - X)(-v_M) + y_P v_m = 0$.

In the final state, the point P is at an angle $\theta$ with the vertical. Its coordinates relative to the center O of the hemisphere are $(a \sin\theta, a \cos\theta)$ (assuming P is to the right of O).
The horizontal position of P is $x_P = X + a \sin\theta$.
Since $x_P$ is constant, and initially $x_P = X_{initial} + a \sin(0) = X_{initial}$, we have $x_P = X_{initial}$.
So, $X_{initial} = X + a \sin\theta$. This means $X - X_{initial} = -a \sin\theta$. The hemisphere moves to the left, which is consistent with the diagram.
The term $(x_P - X)$ represents the horizontal distance of P from the center O. So, $x_P - X = a \sin\theta$.
The term $y_P$ represents the vertical distance of P from the base, which is $a \cos\theta$ (height of P above O).
Substituting these into the differentiated equation:
$(a \sin\theta)(-v_M) + (a \cos\theta)v_m = 0$
$-v_M \sin\theta + v_m \cos\theta = 0$
$v_m = v_M \frac{\sin\theta}{\cos\theta} = v_M \tan\theta$ (Equation 2)

3. Calculate Velocities: Substitute Equation 2 into Equation 1:
$\frac{1}{2} M v_M^2 + \frac{1}{2} m (v_M \tan\theta)^2 = mga(1 - \cos\theta)$
$\frac{1}{2} v_M^2 (M + m \tan^2\theta) = mga(1 - \cos\theta)$
$v_M^2 = \frac{2 mga(1 - \cos\theta)}{M + m \tan^2\theta}$

Given values: $M = 4$ kg, $m = 2$ kg, $a = 2$ m, $\theta = 60°$, $g = 10 \ m/s^2$.
$\cos 60° = 1/2$
$\tan 60° = \sqrt{3}$, so $\tan^2 60° = 3$.
$1 - \cos\theta = 1 - 1/2 = 1/2$.

Substitute the values:
$v_M^2 = \frac{2 \times 2 \times 10 \times 2 \times (1/2)}{4 + 2 \times 3}$
$v_M^2 = \frac{40}{4 + 6} = \frac{40}{10} = 4 \ m^2/s^2$.
So, $|v_M| = 2 \ m/s$.

4. Calculate Angular Speed ($\omega$): The angular speed of point P with respect to the center O of the hemisphere, $\omega$, is related to the velocity of P relative to O.
The velocity of P relative to O is $\vec{v}_{P/O} = \vec{v}_P - \vec{v}_O$.
Since the rod moves vertically, $\vec{v}_P = v_m \hat{j}$.
The hemisphere moves horizontally, so $\vec{v}_O = v_M \hat{i}$.
$\vec{v}_{P/O} = v_m \hat{j} - v_M \hat{i}$.
The magnitude of this relative velocity is $v_{P/O} = \sqrt{v_m^2 + v_M^2}$.
Also, for a point moving on a circle of radius $a$ with angular speed $\omega$, $v_{P/O} = a\omega$.
So, $a\omega = \sqrt{v_m^2 + v_M^2}$.
Using $v_m = v_M \tan\theta$:
$a\omega = \sqrt{(v_M \tan\theta)^2 + v_M^2} = \sqrt{v_M^2 (\tan^2\theta + 1)} = \sqrt{v_M^2 \sec^2\theta} = |v_M \sec\theta|$.
Since $\theta = 60°$, $\sec\theta = \sec 60° = 2$.
$a\omega = |v_M| \sec\theta$.
$\omega = \frac{|v_M| \sec\theta}{a}$.
Substitute $|v_M| = 2 \ m/s$, $a = 2$ m, $\sec\theta = 2$:
$\omega = \frac{2 \times 2}{2} = 2 \ rad/s$.

The final answer is $\boxed{2}$.

Explanation: The problem is solved using the principle of conservation of mechanical energy and kinematic constraints.

1. Conservation of Energy: Since all surfaces are smooth and the guide force does no work, the total mechanical energy of the rod-hemisphere system is conserved. The initial energy (potential energy of the rod at height 'a') is equated to the final energy (kinetic energy of both rod and hemisphere + potential energy of the rod at height 'a cosθ').
2. Kinematic Constraint: The condition that the rod's end P remains on the hemisphere's surface and the rod moves vertically provides a crucial relationship between the velocities of the rod and the hemisphere. This relationship is derived by differentiating the equation of the hemisphere's surface with respect to time, considering the fixed horizontal position of the rod. It leads to $v_m = v_M \tan\theta$.
3. Angular Speed: The angular speed of P with respect to O is the magnitude of the velocity of P relative to O, divided by the radius 'a'. The velocity of P relative to O is found by vector subtraction: $\vec{v}_{P/O} = \vec{v}_P - \vec{v}_O$.

Answer: The angular speed of point P with respect to centre O of the hemisphere is 2 rad/s.