Question
Question: A thin uniform rod of mass m lies on a horizontal table. Find minimum horizontal force that should b...
A thin uniform rod of mass m lies on a horizontal table. Find minimum horizontal force that should be applied to the end of the rod perpendicular to it so that, it can be moved. (Coefficient of friction is
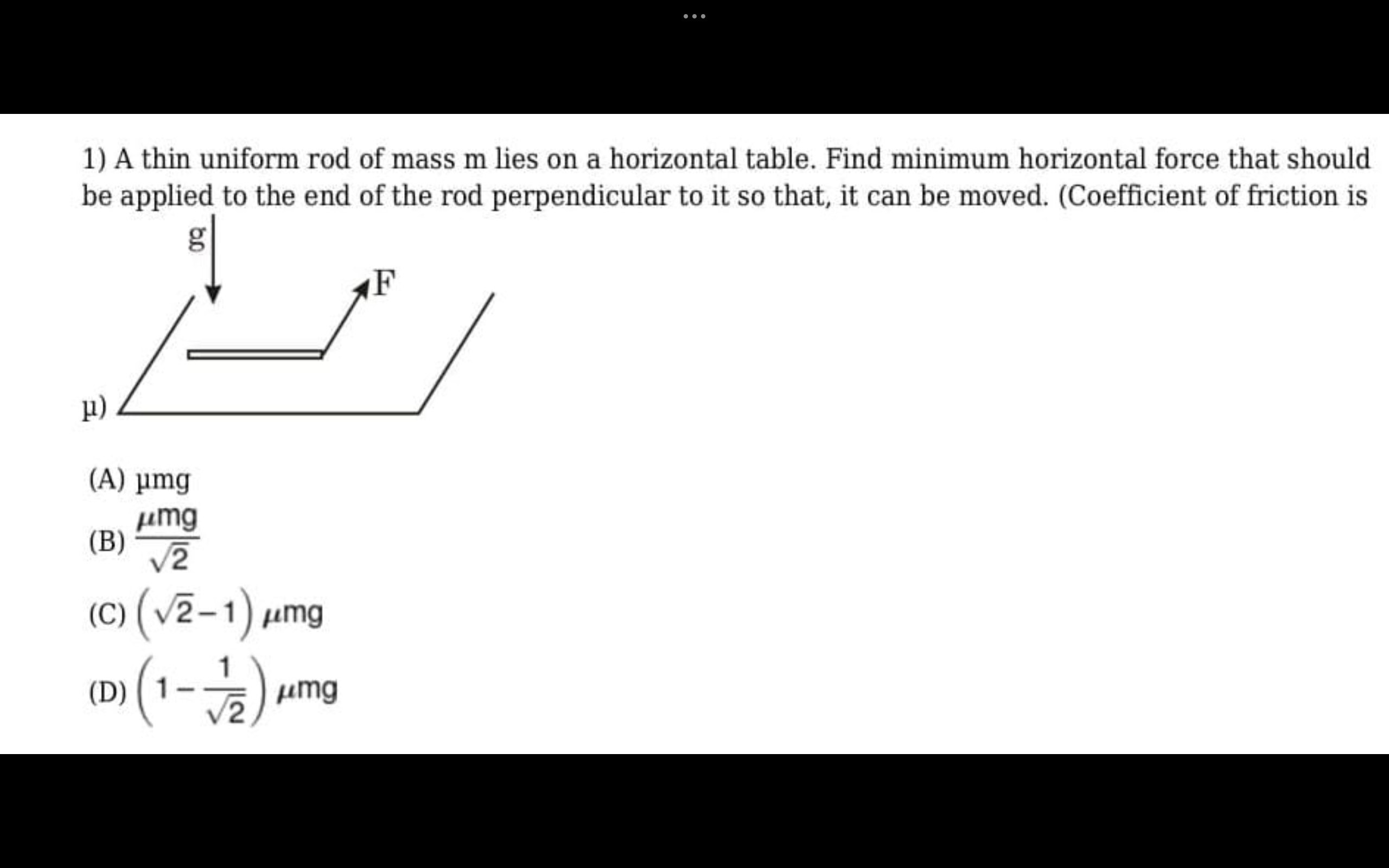
μmg
2μmg
(2−1)μmg
(1−21)μmg
2μmg
Solution
The rod starts to move by rotating about an instantaneous center of rotation (ICOR). For minimum force, this ICOR is located at a specific point on the rod. For a uniform rod of length L and mass m on a rough surface, when a force is applied perpendicularly at one end, the ICOR is at a distance L/(22) from the center of mass, on the side opposite to the applied force.
Let the center of mass be at x=0, so the rod extends from −L/2 to L/2. The force F is applied at x=L/2. The ICOR is at xc=−L/(22).
The condition for impending motion requires that the net force in the direction of the applied force is zero. The friction force at each point opposes the impending motion of that point. Points with x<xc move opposite to points with x>xc.
The total friction force is the sum of friction forces on either side of the ICOR, taking into account their directions.
Summing forces in the direction of F: F+∫−L/2xcμLmgdx−∫xcL/2μLmgdx=0
F+μLmg(xc−(−L/2))−μLmg(L/2−xc)=0
F+μLmg(2xc)=0
Substituting xc=−L/(22): F=−2μLmg(−22L)=2μmg
