Question

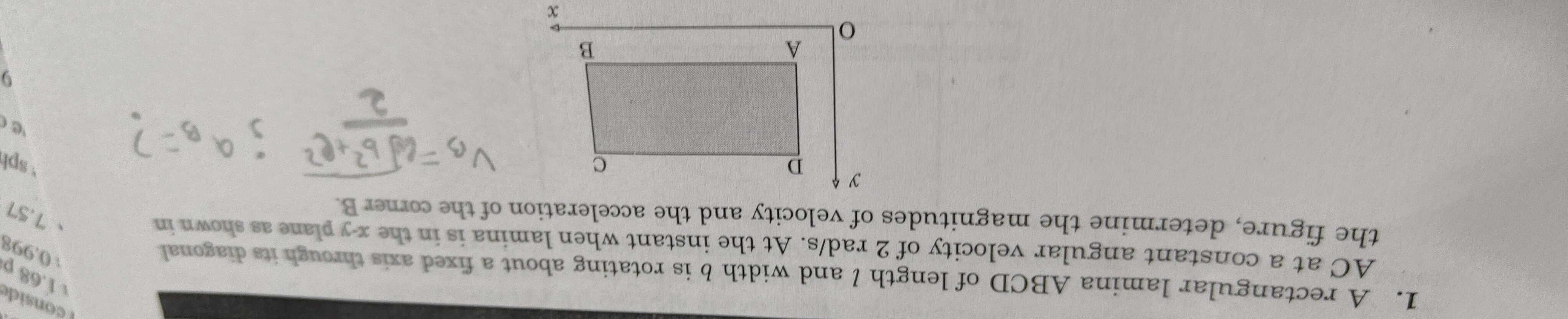
A rectangular lamina ABCD of length l and width b is rotating about a fixed axis through its diagonal AC at a constant angular velocity of 2 rad/s. At the instant when lamina is in the x-y plane as shown in the figure, determine the magnitudes of velocity and the acceleration of the corner B.

Answer 1

V_B = \frac{2lb}{\sqrt{l^2+b^2}}; a_B = \frac{4lb}{\sqrt{l^2+b^2}}

Answer 2

The problem describes a rectangular lamina ABCD of length $l$ and width $b$ rotating about a fixed axis through its diagonal AC with a constant angular velocity $\omega = 2 \text{ rad/s}$. We need to find the magnitudes of velocity and acceleration of corner B.

First, let's establish the coordinates of the vertices of the rectangle. Assuming a standard Cartesian coordinate system, and based on the typical labeling of a rectangle (counter-clockwise or clockwise sequence), let's place vertex A at the origin $(0,0)$. Then, the coordinates of the vertices are: A = $(0,0)$ B = $(l,0)$ (length $l$ along x-axis) C = $(l,b)$ (width $b$ along y-axis) D = $(0,b)$

The axis of rotation is the diagonal AC. This axis passes through A$(0,0)$ and C$(l,b)$. The equation of the line representing the diagonal AC is given by $y - 0 = \frac{b-0}{l-0}(x-0)$, which simplifies to $y = \frac{b}{l}x$, or $bx - ly = 0$.

For a point rotating about a fixed axis, its velocity is $V = \omega r_{\perp}$ and its acceleration is $a = \omega^2 r_{\perp}$ (since $\omega$ is constant, there is no tangential acceleration component due to angular acceleration). Here, $r_{\perp}$ is the perpendicular distance from the point to the axis of rotation.

We need to find the perpendicular distance from corner B$(l,0)$ to the line $bx - ly = 0$. The formula for the perpendicular distance from a point $(x_0, y_0)$ to a line $Ax + By + C = 0$ is $d = \frac{|Ax_0 + By_0 + C|}{\sqrt{A^2 + B^2}}$. For point B$(l,0)$ and line $bx - ly = 0$: $r_{\perp} = \frac{|b(l) - l(0)|}{\sqrt{b^2 + (-l)^2}} = \frac{|bl|}{\sqrt{b^2 + l^2}} = \frac{bl}{\sqrt{l^2 + b^2}}$.

Alternatively, consider the right-angled triangle ABC. The area of this triangle is $\frac{1}{2} \times \text{base} \times \text{height} = \frac{1}{2} \times AB \times BC = \frac{1}{2} lb$. Also, the area can be expressed as $\frac{1}{2} \times AC \times r_{\perp}$, where $AC$ is the length of the diagonal and $r_{\perp}$ is the perpendicular distance from B to AC. The length of the diagonal $AC = \sqrt{l^2 + b^2}$. So, $\frac{1}{2} \sqrt{l^2 + b^2} \times r_{\perp} = \frac{1}{2} lb$. This gives $r_{\perp} = \frac{lb}{\sqrt{l^2 + b^2}}$.

Now, we can calculate the magnitudes of velocity and acceleration of corner B. The angular velocity is given as $\omega = 2 \text{ rad/s}$.

1. Magnitude of Velocity of corner B ($V_B$): $V_B = \omega r_{\perp}$ $V_B = \omega \frac{lb}{\sqrt{l^2 + b^2}}$ Substituting $\omega = 2 \text{ rad/s}$: $V_B = \frac{2lb}{\sqrt{l^2 + b^2}}$

2. Magnitude of Acceleration of corner B ($a_B$): Since the angular velocity $\omega$ is constant, there is no angular acceleration $(\vec{\alpha} = \frac{d\vec{\omega}}{dt} = 0)$. Therefore, the acceleration of point B is entirely centripetal acceleration, directed towards the axis of rotation. $a_B = \omega^2 r_{\perp}$ $a_B = \omega^2 \frac{lb}{\sqrt{l^2 + b^2}}$ Substituting $\omega = 2 \text{ rad/s}$: $a_B = (2)^2 \frac{lb}{\sqrt{l^2 + b^2}}$ $a_B = \frac{4lb}{\sqrt{l^2 + b^2}}$

The question provides an expression $V_B = \sqrt{\omega^2b^2+l^2}$ which is dimensionally inconsistent $(\sqrt{(\text{L/T})^2 + \text{L}^2})$, suggesting a possible typo in the provided hint. Our derived velocity $V_B = \frac{2lb}{\sqrt{l^2 + b^2}}$ is dimensionally correct and derived from fundamental principles of rotational motion.

Explanation of the solution:

1. Identify the fixed axis of rotation: The diagonal AC.
2. Determine the perpendicular distance ($r_{\perp}$) from the point B to the axis AC. This can be done using the formula for the distance from a point to a line, or by using the area of the triangle ABC.
3. Apply the formula for velocity in rotational motion: $V_B = \omega r_{\perp}$.
4. Apply the formula for acceleration in rotational motion: $a_B = \omega^2 r_{\perp}$ (since angular velocity is constant, there is only centripetal acceleration).
5. Substitute the given value of $\omega = 2 \text{ rad/s}$.