Question

A particle of mass 1 kg is subjected to a force which depends on the position as $\vec{F} = -k(x\hat{i} + y\hat{j})kgms^{-2}$ with $k = 1 kgs^{-2}$. At time $t = 0$, the particle's position $\vec{r} = (\frac{1}{\sqrt{2}}\hat{i} + \sqrt{2}\hat{j})m$ and its velocity $\vec{v} = (-\sqrt{2}\hat{i} + \sqrt{2}\hat{j} + \frac{2}{\pi}\hat{k})ms^{-1}$. Let $v_x$ and $v_y$ denote the $x$ and the $y$ components of the particle's velocity, respectively. Ignore gravity. When $z = 0.5$ m, the value of $(x v_y - y v_x)$ is _______ $m^2s^{-1}$.

Answer 1

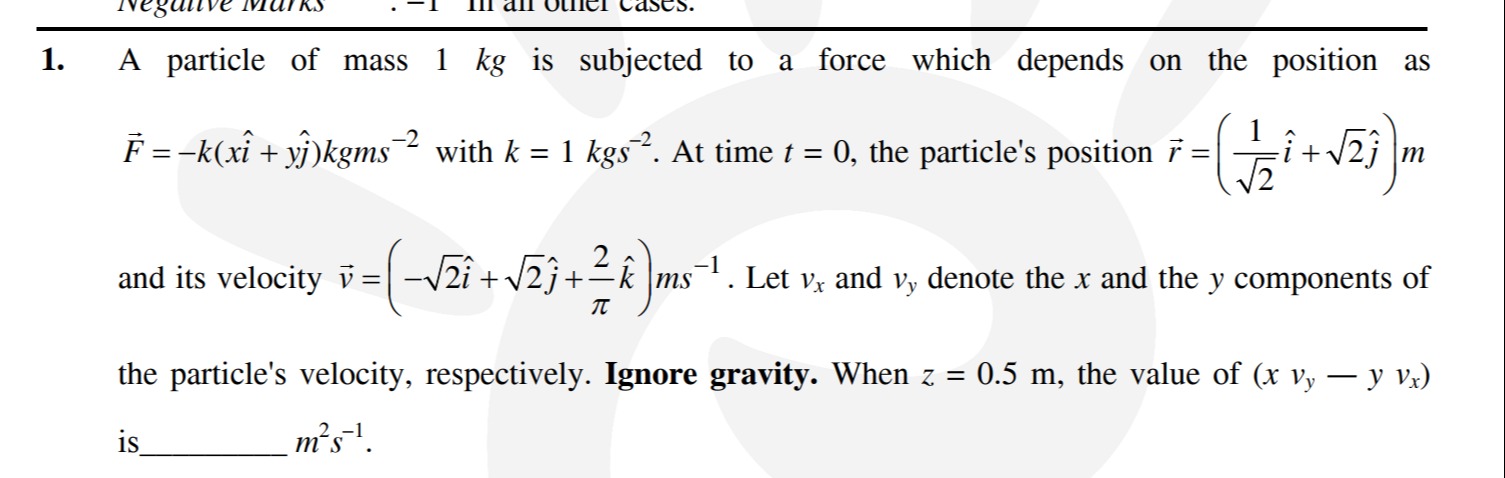
3

Answer 2

The force acting on the particle is $\vec{F} = -k(x\hat{i} + y\hat{j})$. This force is directed towards the origin in the xy-plane. The torque about the z-axis due to this force is calculated as $\vec{\tau}_z = \vec{r}_{xy} \times \vec{F}$, where $\vec{r}_{xy} = x\hat{i} + y\hat{j}$. This calculation shows that $\vec{\tau}_z = \vec{0}$. Since the z-component of the torque is zero, the z-component of the angular momentum, $L_z = m(x v_y - y v_x)$, is conserved. We calculate the initial value of $(x v_y - y v_x)$ at $t=0$ using the given initial position and velocity. This initial value is $3$. Since $L_z$ is conserved and $m=1$, the value of $(x v_y - y v_x)$ is constant and equal to 3 for all times. Therefore, when $z=0.5$ m, the value of $(x v_y - y v_x)$ is 3.