Question

A body of elliptical cross - section is made up of material of refractive index n₂. The body is surrounded by a liquid of refractive index n₁. The figure here shows a cross - section of this body. If any ray parallel to major axis of the cross - section passes through focus of the cross - section (as shown), then the eccentricity of the elliptical cross - section is

• A. $\frac{n_1}{n_2}$
• B. $\frac{1}{\sqrt{n_1n_2}}$
• C. $\frac{2}{n_1 + n_2}$
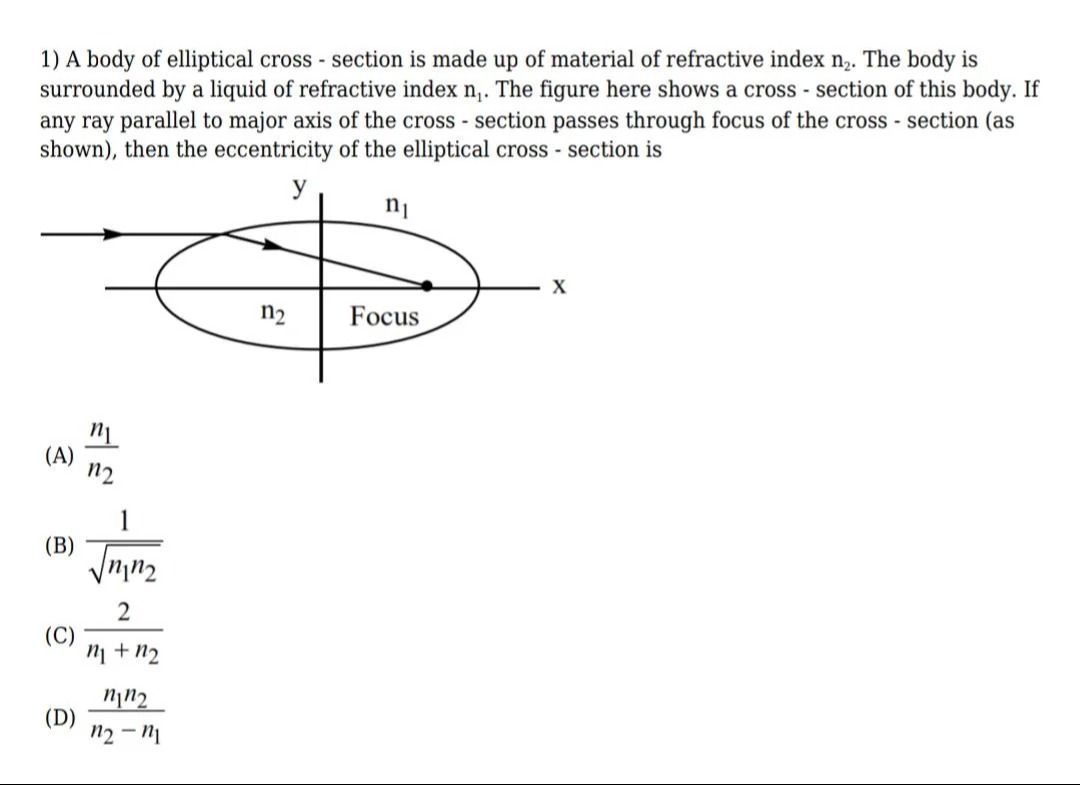
• D. $\frac{n_1n_2}{n_2 - n_1}$

Answer 1

Answer: (A)

$\frac{n_1}{n_2}$

Answer 2

The problem describes an elliptical cross-section made of material with refractive index $n_2$, surrounded by a liquid of refractive index $n_1$. A ray parallel to the major axis of the ellipse, after refracting at the boundary, passes through a focus of the ellipse. We need to find the eccentricity of the ellipse.

This is a classic problem related to the optical properties of conic sections, specifically how they act as aplanatic surfaces or Cartesian ovals.

Key Concept:

For a refracting surface to perfectly focus parallel rays to a point (or for rays from a point source to emerge as parallel rays), the optical path length from a wavefront to the focus must be constant. This condition defines a Cartesian oval.

Let the elliptical cross-section be described by the equation $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$, where $a$ is the semi-major axis and $b$ is the semi-minor axis. The foci of the ellipse are at $(\pm ae, 0)$, where $e$ is the eccentricity.

Assume the parallel rays are incident from the left (from $x = -\infty$) along the positive x-axis, and they converge to the right focus $F(ae, 0)$. Let $P(x, y)$ be any point on the elliptical boundary where a ray strikes.

The optical path length from an initial plane wavefront (e.g., at $x = x_0$, where $x_0 \ll x$) to the point $P(x, y)$ is $n_1(x - x_0)$. The optical path length from the point $P(x, y)$ to the focus $F(ae, 0)$ is $n_2 \cdot PF$.

For all parallel rays to converge to the focus, the total optical path length must be constant: $n_1(x - x_0) + n_2 \cdot PF = \text{Constant}$ Since $n_1 x_0$ is a constant, we can absorb it into the right-hand side, so: $n_1 x + n_2 \cdot PF = \text{Constant}'$

For an ellipse, the distance from any point $P(x, y)$ on the ellipse to a focus $F(ae, 0)$ is given by $PF = a - ex$. (This is a standard property: for the right focus, $PF = a - ex$; for the left focus $F'(-ae, 0)$, $PF' = a + ex$).

Substitute $PF = a - ex$ into the equation: $n_1 x + n_2 (a - ex) = \text{Constant}'$ $n_1 x + n_2 a - n_2 ex = \text{Constant}'$ Rearrange the terms: $(n_1 - n_2 e)x + n_2 a = \text{Constant}'$

For this equation to hold true for any point $P(x, y)$ on the ellipse (i.e., for any value of $x$ on the ellipse), the coefficient of $x$ must be zero. Therefore: $n_1 - n_2 e = 0$ $n_1 = n_2 e$ $e = \frac{n_1}{n_2}$

For the body to be an ellipse, its eccentricity $e$ must be less than 1 ($e < 1$). This implies $n_1/n_2 < 1$, or $n_1 < n_2$. This condition means the light is going from a rarer medium to a denser medium, which is typical for a converging lens.

The final answer is $\frac{n_1}{n_2}$.