Question

a, b are real numbers such that |a – 1| + |b – 1| = |a| + |b| = |a + 1| + |b + 1|, then value of |a – b| can be :-

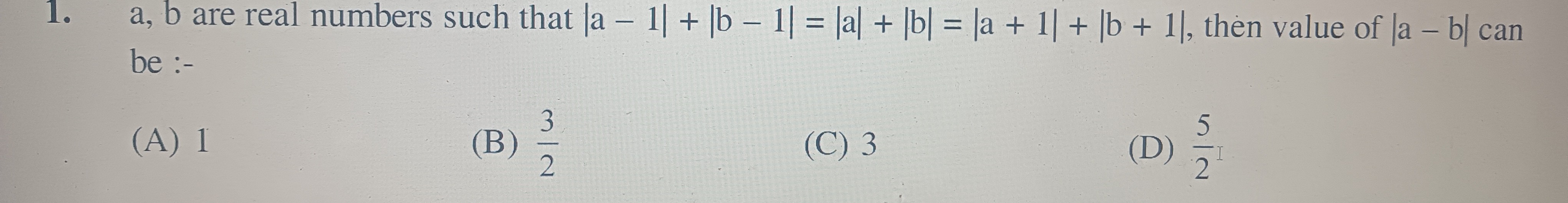
• A. 1
• B. 3/2
• C. 3
• D. 5/2

Answer 1

Answer: (C)

3

Answer 2

The given conditions are:

1. $|a – 1| + |b – 1| = |a| + |b|$
2. $|a| + |b| = |a + 1| + |b + 1|$

From $|x-c| + |x| \ge |c|$, equality holds if and only if $x$ is between $0$ and $c$. For the first equation, $|a-1| + |a| \ge 1$ and $|b-1| + |b| \ge 1$. The equality $|a-1| + |a| = |a| + |a-1|$ implies that either $a \in [0, 1]$ and $b \in [0, 1]$, or one of $a, b$ is in $[0, 1]$ and the other is outside $[0, 1]$ in such a way that the sum of distances is maintained. A more direct analysis of $|x-1| + |x| = |y-1| + |y|$ shows that it implies either ($a \ge 1$ and $b \le 0$) or ($a \le 0$ and $b \ge 1$) or ($0 \le a \le 1$ and $0 \le b \le 1$ and $a+b=1$).

For the second equation, $|a| + |a+1| \ge 1$ and $|b| + |b+1| \ge 1$. The equality $|a| + |a+1| = |b| + |b+1|$ implies that either ($a \ge 0$ and $b \le -1$) or ($a \le -1$ and $b \ge 0$) or ($-1 \le a \le 0$ and $-1 \le b \le 0$ and $a+b=-1$).

Combining these conditions, we find the valid pairs $(a,b)$ are:

• $a \ge 1$ and $b \le -1$.
• $a \le -1$ and $b \ge 1$.

If $a \ge 1$ and $b \le -1$: Then $a$ is positive and $b$ is negative. $|a-b| = a - b$. Since $a \ge 1$ and $b \le -1$, $a-b \ge 1 - (-1) = 2$. Let $a=1$ and $b=-2$. $|1-1| + |-2-1| = 0 + 3 = 3$. $|1| + |-2| = 1 + 2 = 3$. $|1+1| + |-2+1| = |2| + |-1| = 2 + 1 = 3$. The conditions are satisfied. For this pair, $|a-b| = |1 - (-2)| = |3| = 3$.

If $a \le -1$ and $b \ge 1$: Then $a$ is negative and $b$ is positive. $|a-b| = b - a$. Since $b \ge 1$ and $a \le -1$, $b-a \ge 1 - (-1) = 2$. Let $a=-2$ and $b=1$. $|-2-1| + |1-1| = |-3| + 0 = 3$. $|-2| + |1| = 2 + 1 = 3$. $|-2+1| + |1+1| = |-1| + |2| = 1 + 2 = 3$. The conditions are satisfied. For this pair, $|a-b| = |-2 - 1| = |-3| = 3$.

In both valid cases, $|a-b| \ge 2$. We have found a specific instance where $|a-b|=3$.