Question

If instantaneous current in a circuit is given by $I = (2 + 3 \sin \omega t)A$, then the effective value of resulting current in the circuit is :-

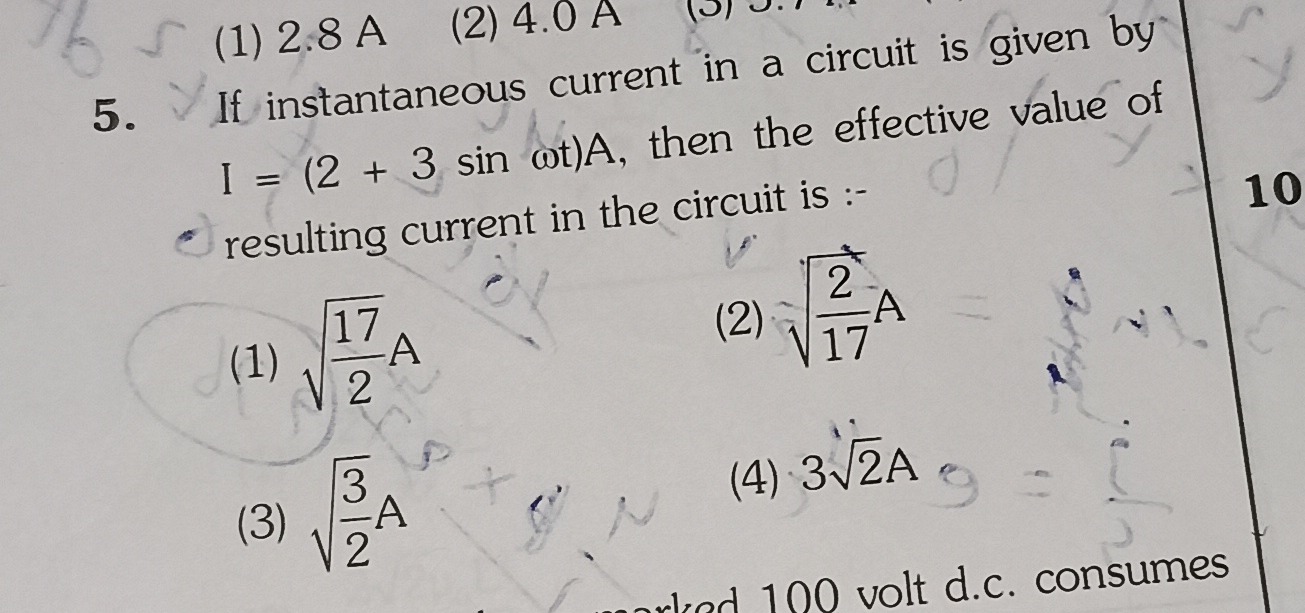
• A. $\sqrt{\frac{17}{2}}A$
• B. $\sqrt{\frac{2}{17}}A$
• C. $\sqrt{\frac{3}{2}}A$
• D. $3\sqrt{2}A$

Answer 1

Answer: (A)

The effective value of the resulting current in the circuit is $\sqrt{\frac{17}{2}}A$.

Answer 2

The instantaneous current is given by $I = (2 + 3 \sin \omega t)A$. This current can be decomposed into a DC component and an AC component. The DC component is $I_{DC} = 2$ A. The AC component is $I_{AC} = 3 \sin \omega t$. The amplitude of this AC component is $I_m = 3$ A. The RMS value of the AC component is $I_{rms(AC)} = \frac{I_m}{\sqrt{2}} = \frac{3}{\sqrt{2}}$ A. The effective value (RMS value) of a current that has both DC and AC components is given by the formula: $I_{eff} = \sqrt{I_{DC}^2 + I_{rms(AC)}^2}$. Substituting the values: $I_{eff} = \sqrt{(2)^2 + \left(\frac{3}{\sqrt{2}}\right)^2} = \sqrt{4 + \frac{9}{2}} = \sqrt{\frac{8}{2} + \frac{9}{2}} = \sqrt{\frac{17}{2}}$ A.