Question

The solution of the differential equation $\frac{dy}{dx} = tan(\frac{y}{x})+\frac{y}{x}$ is [2017]

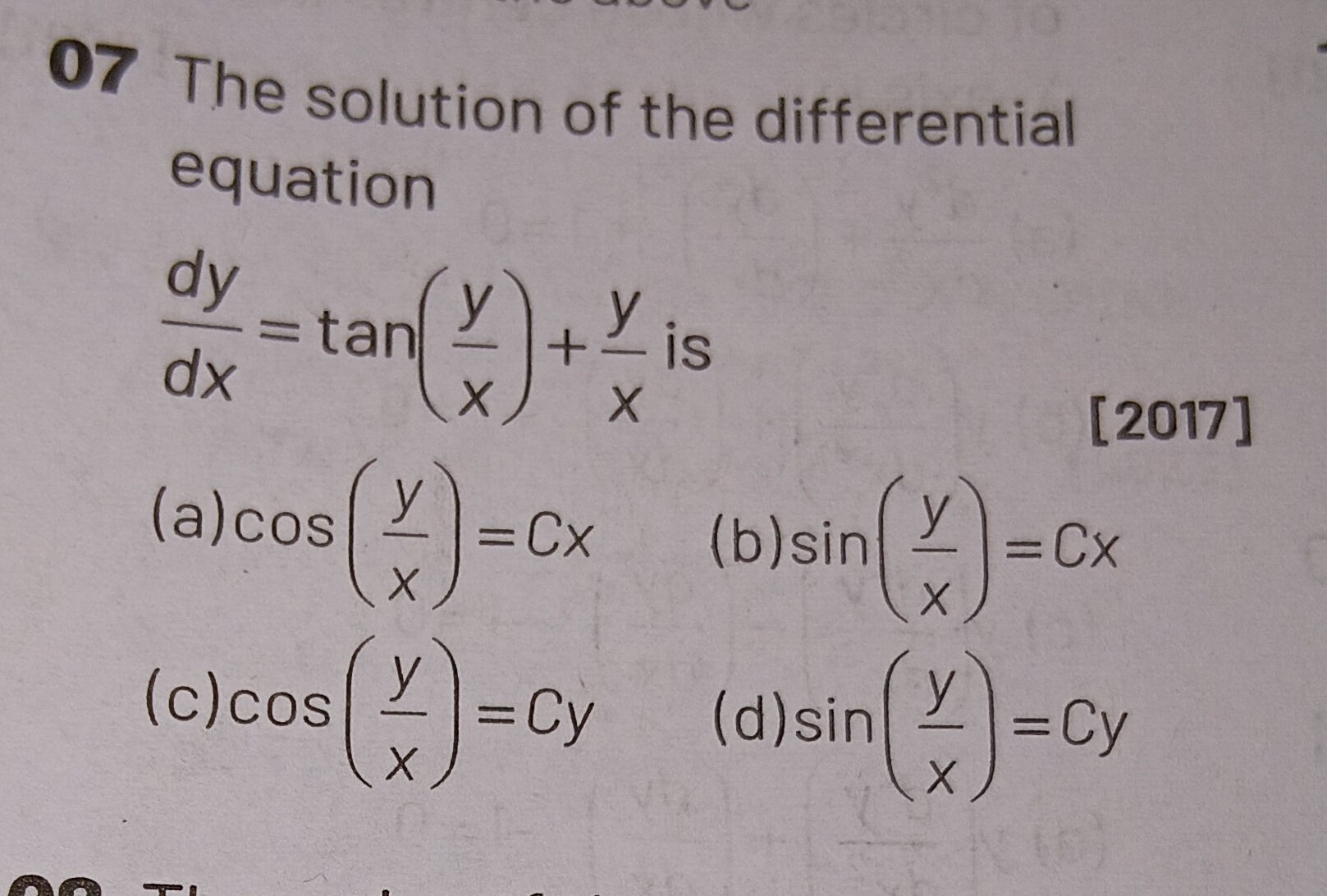
• A. $cos(\frac{y}{x})=Cx$
• B. $sin(\frac{y}{x})=Cx$
• C. $cos(\frac{y}{x})=Cy$
• D. $sin(\frac{y}{x})=Cy$

Answer 1

Answer: (B)

$\sin\left(\frac{y}{x}\right) = Cx$

Answer 2

Given the differential equation

$$\frac{dy}{dx} = \tan\left(\frac{y}{x}\right) + \frac{y}{x}$$

substitute $v = \frac{y}{x}$, so that $y = vx$ and $\frac{dy}{dx} = v + x\frac{dv}{dx}$. Then,

$$v + x\frac{dv}{dx} = \tan(v) + v \implies x\frac{dv}{dx} = \tan(v).$$

Separate the variables:

$$\frac{dv}{\tan(v)} = \frac{dx}{x}.$$

Since $\frac{1}{\tan(v)} = \cot(v)$, we have

$$\cot(v) dv = \frac{dx}{x}.$$

Integrating both sides,

$$\int \cot(v) dv = \int \frac{dx}{x} \quad \Longrightarrow \quad \ln|\sin(v)| = \ln|x| + C,$$

or

$$\ln\left|\frac{\sin v}{x}\right| = C.$$

Exponentiating,

$$\frac{\sin v}{x} = C_1 \quad \Longrightarrow \quad \sin\left(\frac{y}{x}\right) = Cx,$$

where $C$ is an arbitrary constant.