Question

Let the area of the triangle formed by the lines $x+2=y-1=z, \frac{x-3}{5} = \frac{y}{-1} = \frac{z-1}{1}$ and $\frac{x}{-3} = \frac{y-3}{3} = \frac{z-2}{1}$ be A. Then A$^2$ is equal to _______.

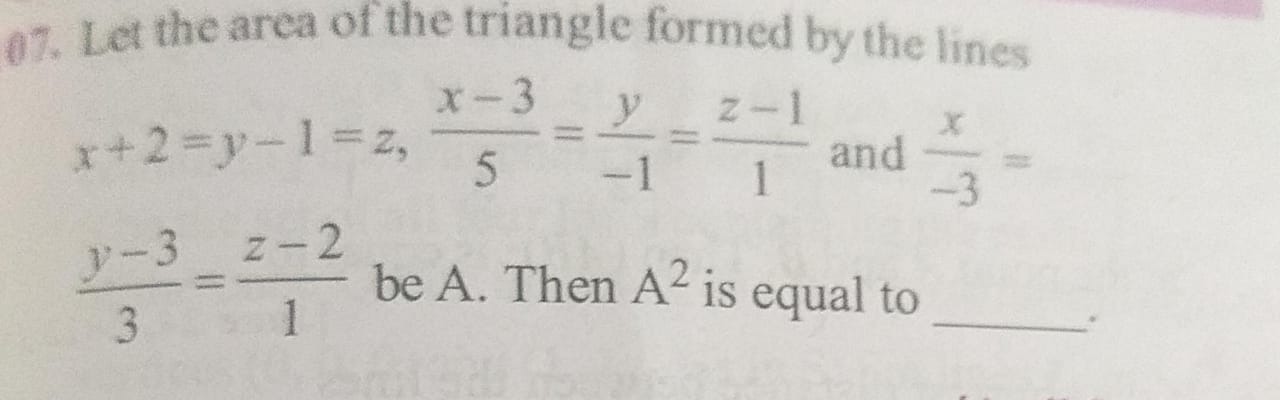
Answer 1

56

Answer 2

The vertices of the triangle are the pairwise intersection points of the given lines. Line 1: $\vec{r}_1 = (-2, 1, 0) + t_1(1, 1, 1)$. Line 2: $\vec{r}_2 = (3, 0, 1) + t_2(5, -1, 1)$. Line 3: $\vec{r}_3 = (0, 3, 2) + t_3(-3, 3, 1)$.

Intersection of Line 1 and Line 2: $V_{12} = (-2, 1, 0)$. Intersection of Line 1 and Line 3: $V_{13} = (0, 3, 2)$. Intersection of Line 2 and Line 3: $V_{23} = (3, 0, 1)$.

Vectors representing two sides of the triangle: $\vec{u} = V_{13} - V_{12} = (2, 2, 2)$. $\vec{v} = V_{23} - V_{12} = (5, -1, 1)$.

Cross product: $\vec{u} \times \vec{v} = (4, 8, -12)$. Magnitude of cross product: $||\vec{u} \times \vec{v}|| = \sqrt{4^2 + 8^2 + (-12)^2} = \sqrt{16 + 64 + 144} = \sqrt{224}$.

Area of triangle $A = \frac{1}{2} ||\vec{u} \times \vec{v}|| = \frac{1}{2} \sqrt{224}$. $A^2 = \left(\frac{1}{2} \sqrt{224}\right)^2 = \frac{1}{4} \times 224 = 56$.