Question

Let the latus rectum of the hyperbola, $\frac{x^2}{9}-\frac{y^2}{b^2}=1$ subtend an angle of $\frac{\pi}{3}$ at the centre of the hyperbola. If $b^2$ is equal to $\frac{l}{m}(1+\sqrt{n})$, where $l$ and $m$ are co-prime numbers, then $l^2 + m^2 + n^2$ is equal to

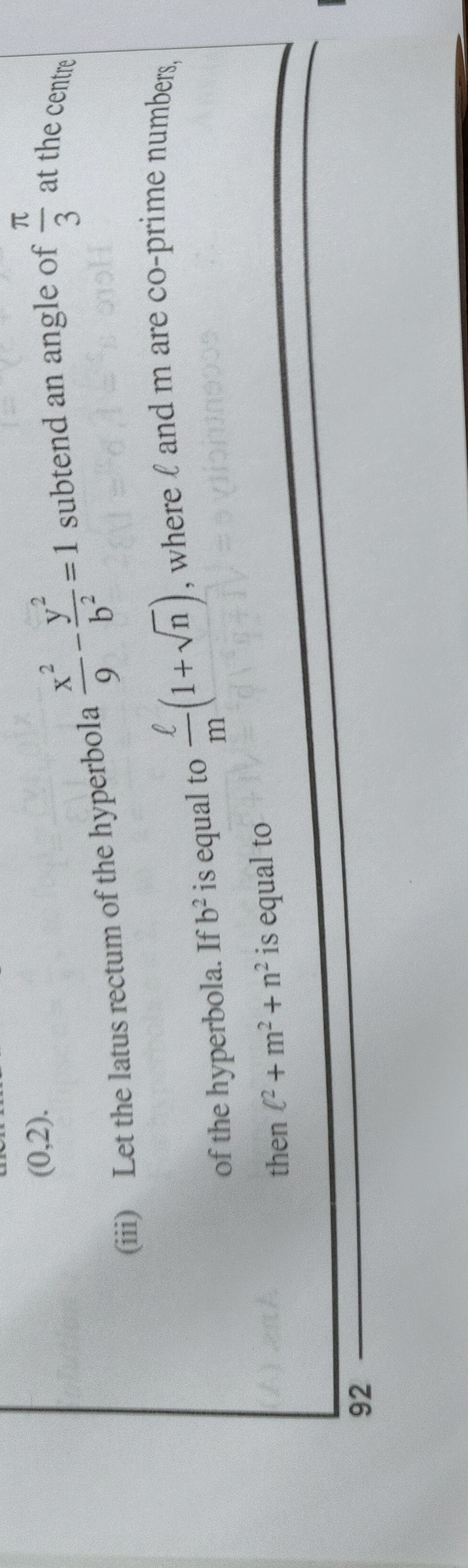
• A. 182
• B. 178
• C. 180
• D. 176

Answer 1

Answer: (A)

182

Answer 2

The latus rectum of the hyperbola $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ has endpoints at $(ae, \pm \frac{b^2}{a})$. The angle subtended by the latus rectum at the center $(0,0)$ is $2\phi$, where $\tan \phi = \frac{b^2/a}{ae} = \frac{b^2}{a^2e}$. Given this angle is $\frac{\pi}{3}$, we have $2\phi = \frac{\pi}{3}$, so $\phi = \frac{\pi}{6}$. Thus, $\tan(\frac{\pi}{6}) = \frac{1}{\sqrt{3}} = \frac{b^2}{a^2e}$. This implies $a^2e = b^2\sqrt{3}$. Squaring both sides, we get $a^4e^2 = 3b^4$. Using the eccentricity formula $e^2 = 1 + \frac{b^2}{a^2}$, we substitute it into the equation: $a^4(1 + \frac{b^2}{a^2}) = 3b^4$, which simplifies to $a^4 + a^2b^2 = 3b^4$. Given $a^2 = 9$, we have $9^2 + 9b^2 = 3b^4$, so $81 + 9b^2 = 3b^4$. Dividing by 3 gives $b^4 - 3b^2 - 27 = 0$. Let $X = b^2$. The quadratic equation becomes $X^2 - 3X - 27 = 0$. Solving for $X$ using the quadratic formula, $X = \frac{3 \pm \sqrt{(-3)^2 - 4(1)(-27)}}{2} = \frac{3 \pm \sqrt{9+108}}{2} = \frac{3 \pm \sqrt{117}}{2}$. Since $b^2$ must be positive, $b^2 = \frac{3 + \sqrt{117}}{2}$. Simplifying $\sqrt{117} = \sqrt{9 \times 13} = 3\sqrt{13}$, we get $b^2 = \frac{3 + 3\sqrt{13}}{2} = \frac{3}{2}(1+\sqrt{13})$. Comparing this with $b^2 = \frac{l}{m}(1+\sqrt{n})$, we find $l=3$, $m=2$, and $n=13$. $l$ and $m$ are co-prime. Finally, we calculate $l^2 + m^2 + n^2 = 3^2 + 2^2 + 13^2 = 9 + 4 + 169 = 182$.