Question

A satellite is revolving around a planet in a circular orbit close to its surface. Let '$\rho$' be the mean density and 'R' be the radius of the planet. Then the period of the satellite is (G = universal constant of gravitation)

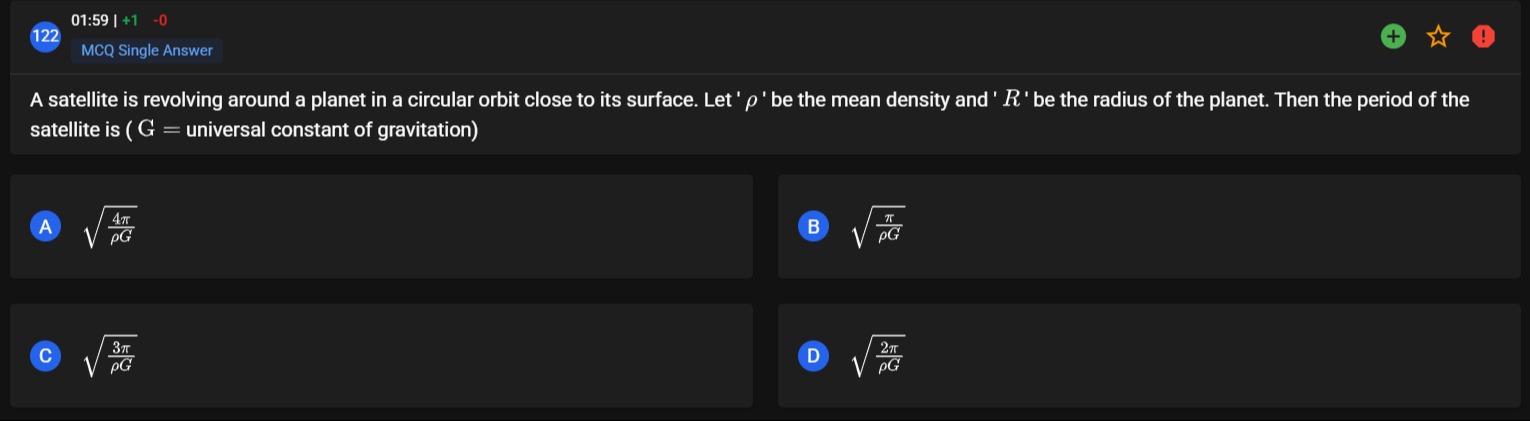
• A. $\sqrt{\frac{4\pi}{\rho G}}$
• B. $\sqrt{\frac{\pi}{\rho G}}$
• C. $\sqrt{\frac{3\pi}{\rho G}}$
• D. $\sqrt{\frac{2\pi}{\rho G}}$

Answer 1

Answer: (C)

$\sqrt{\frac{3\pi}{\rho G}}$

Answer 2

For a satellite in a circular orbit of radius R (planet's surface), the time period is

$$T = 2\pi\sqrt{\frac{R^3}{GM}}$$

The planet's mass $M$ is given by

$$M = \rho \cdot \frac{4}{3}\pi R^3$$

Substitute $M$ into the period formula:

$$T = 2\pi\sqrt{\frac{R^3}{G\left(\rho\cdot\frac{4}{3}\pi R^3\right)}} = 2\pi\sqrt{\frac{1}{G\rho\cdot\frac{4}{3}\pi}} = 2\pi\sqrt{\frac{3}{4\pi G\rho}}$$

Simplify:

$$T = \sqrt{\frac{4\pi^2\cdot 3}{4\pi G\rho}} = \sqrt{\frac{3\pi}{G\rho}}$$

Thus, the correct answer is Option C.