Question

Four electric charges +q, +q, -q and -q are placed in order at the corners of a square of side 2 L. The electric potential at point midway between the two positive charges is

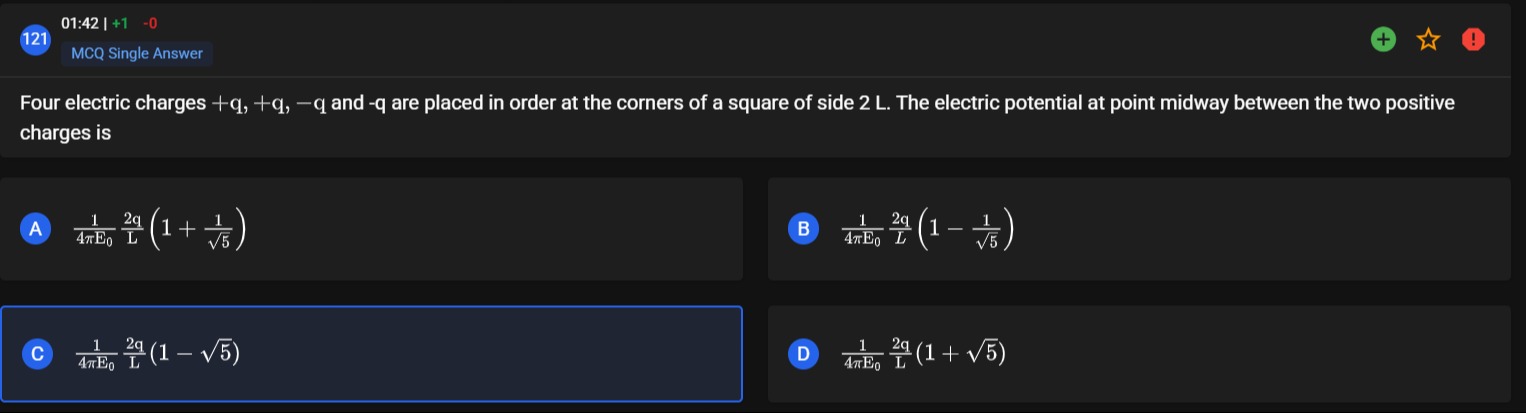
• A. $\frac{1}{4\pi E_0} \frac{2q}{L} (1 + \frac{1}{\sqrt{5}})$
• B. $\frac{1}{4\pi E_0} \frac{2q}{L} (1 - \frac{1}{\sqrt{5}})$
• C. $\frac{1}{4\pi E_0} \frac{2q}{L} (1 - \sqrt{5})$
• D. $\frac{1}{4\pi E_0} \frac{2q}{L} (1 + \sqrt{5})$

Answer 1

Answer: (B)

$\frac{1}{4\pi E_0} \frac{2q}{L} (1 - \frac{1}{\sqrt{5}})$

Answer 2

The electric potential at a point due to a point charge is given by:

$V = \frac{1}{4\pi\epsilon_0} \frac{q}{r}$

Where:

• $V$ is the electric potential
• $q$ is the charge
• $r$ is the distance from the charge to the point

1. Distances:

   • The two +q charges are at a distance $L$ from the midpoint.
   • The two -q charges are at a distance $\sqrt{L^2 + (2L)^2} = \sqrt{5}L$ from the midpoint.

2. Individual Potentials:

   • Potential due to each +q charge: $V_+ = \frac{1}{4\pi\epsilon_0} \frac{q}{L}$
   • Potential due to each -q charge: $V_- = -\frac{1}{4\pi\epsilon_0} \frac{q}{\sqrt{5}L}$

3. Total Potential: The total potential $V$ is the sum of the potentials due to all charges:

   $V = 2V_+ + 2V_- = 2\left(\frac{1}{4\pi\epsilon_0} \frac{q}{L}\right) + 2\left(-\frac{1}{4\pi\epsilon_0} \frac{q}{\sqrt{5}L}\right)$

   $V = \frac{1}{4\pi\epsilon_0} \frac{2q}{L} \left(1 - \frac{1}{\sqrt{5}}\right)$