Question

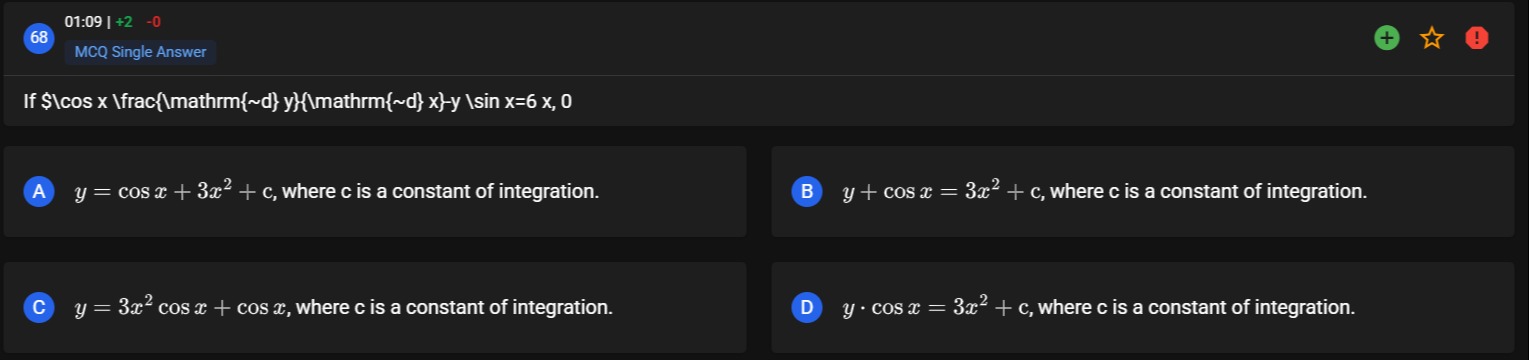
If $\cos x \frac{\mathrm{~d} y}{\mathrm{~d} x}-y \sin x=6 x, 0$

• A. $y = \cos x + 3x^2 + c$, where c is a constant of integration.
• B. $y + \cos x = 3x^2 + c$, where c is a constant of integration.
• C. $y = 3x^2 \cos x + \cos x$, where c is a constant of integration.
• D. $y \cdot \cos x = 3x^2 + c$, where c is a constant of integration.

Answer 1

Answer: (D)

Option D: $y \cdot \cos x = 3x^2 + c$, where c is a constant of integration.

Answer 2

Recognize that the left side is the derivative of $y\cos x$ (by the product rule):

$\frac{d}{dx}[y\cos x] = \frac{dy}{dx} \cos x - y \sin x$.

Thus, the ODE becomes:

$\frac{d}{dx}[y\cos x] = 6x$.

Integrating both sides:

$y\cos x = \int 6x\,dx = 3x^2 + C$.