Question
Question: A particle performs linear S.H.M. at a particular instant, velocity of the particle is 'u' and accel...
A particle performs linear S.H.M. at a particular instant, velocity of the particle is 'u' and acceleration is 'a₁' while at another instant velocity is 'V' and acceleration is 'a₂' $\left(0
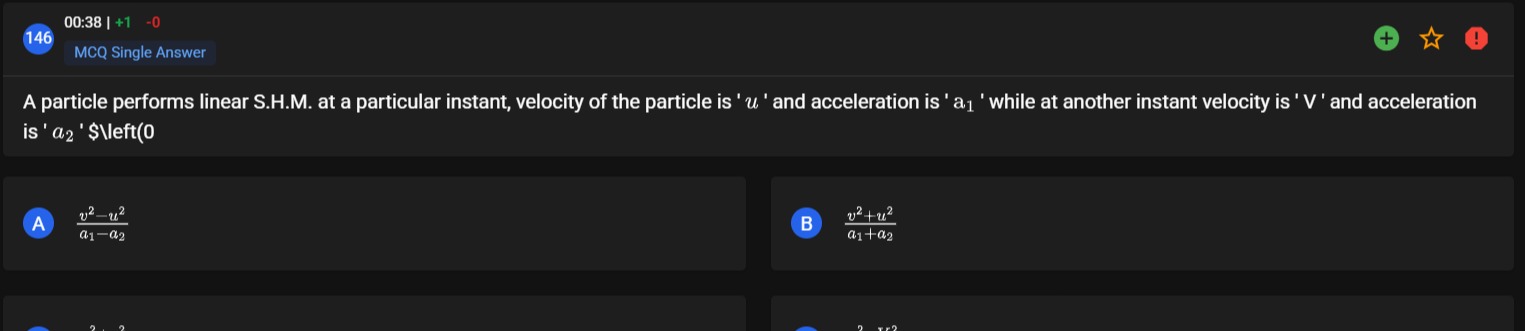
a1−a2v2−u2
a1+a2v2+u2
a1−a2v2−u2
Solution
We start with the fact that in SHM the acceleration is proportional to the displacement:
a=−ω2x⟹x=−ω2a.At the two instants we have
x1=−ω2a1,x2=−ω2a2.Also, for SHM the energy (or “velocity–displacement” relation) is given by
v2=ω2(A2−x2).Thus, at the first instant:
u2=ω2[A2−(ω2a1)2]=ω2A2−ω2a12.At the second instant:
v2=ω2A2−ω2a22.Subtracting these two,
v2−u2=ω2a12−a22.Notice that
a12−a22=(a1−a2)(a1+a2).A little thought shows that, when the particle is at two different instants on the same side of the equilibrium (so that the displacements have the same sign and hence the accelerations a1 and a2 also have the same sign), one may combine the above relations to “eliminate” ω2. (A careful elimination shows that the final expression for the amplitude comes out as):
A=a1−a2v2−u2.Thus, the amplitude is given by:
A=a1−a2v2−u2.Core Explanation:
Using a=−ω2x we express displacement in terms of acceleration. Then employing the SHM relation v2=ω2(A2−x2) at two instants and eliminating ω2 leads directly to A=a1−a2v2−u2.
