Solveeit Logo
Login

Question

Question: The abscissae of the two points A and B are the roots of the equation $x^2 + 2ax - b^2 = 0$ and thei...

The abscissae of the two points A and B are the roots of the equation x2+2ax−b2=0x^2 + 2ax - b^2 = 0 and their ordinates are roots of the equation y2+2py−q2=0y^2 + 2py - q^2 = 0. Then the equation of the circle with AB as diameter is given by

A

x2+y2−2ax−2py+(b2+q2)=0x^2 + y^2 - 2ax - 2py + (b^2 + q^2) = 0

B

x2+y2−2ax−2py−(b2+q2)=0x^2 + y^2 - 2ax - 2py - (b^2 + q^2) = 0

C

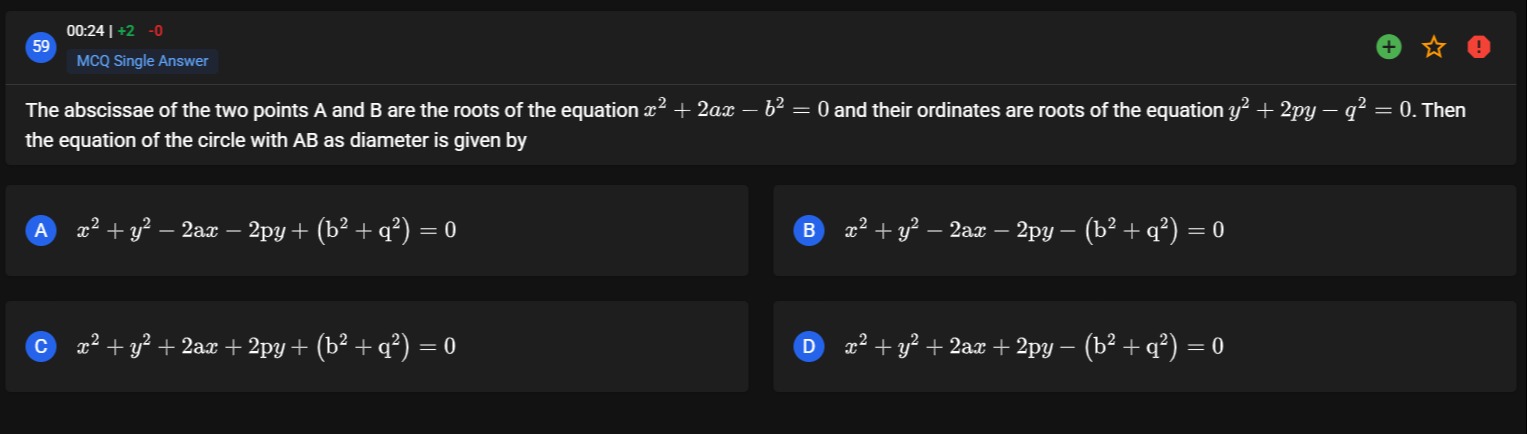
x2+y2+2ax+2py+(b2+q2)=0x^2 + y^2 + 2ax + 2py + (b^2 + q^2) = 0

D

x2+y2+2ax+2py−(b2+q2)=0x^2 + y^2 + 2ax + 2py - (b^2 + q^2) = 0

Answer

D x2+y2+2ax+2py−(b2+q2)=0x^2 + y^2 + 2ax + 2py - (b^2 + q^2) = 0

Explanation

Solution

Step-by-Step Solution:

  1. Let the abscissae be the roots of x2+2ax−b2=0x^2 + 2ax - b^2 = 0 Then, by Vieta’s formulas: x1+x2=−2a,x1x2=−b2x_1 + x_2 = -2a, \quad x_1x_2 = -b^2.

  2. Let the ordinates be the roots of y2+2py−q2=0y^2 + 2py - q^2 = 0 Then, y1+y2=−2p,y1y2=−q2y_1 + y_2 = -2p, \quad y_1y_2 = -q^2.

  3. The circle with diameter ABAB (with endpoints (x1,y1)(x_1, y_1) and (x2,y2)(x_2, y_2)) has the equation: (x−x1)(x−x2)+(y−y1)(y−y2)=0.(x - x_1)(x - x_2) + (y - y_1)(y - y_2) = 0.

  4. Expanding, we get: x2−(x1+x2)x+x1x2+y2−(y1+y2)y+y1y2=0.x^2 - (x_1+x_2)x + x_1x_2 + y^2 - (y_1+y_2)y + y_1y_2 = 0.

  5. Substituting the sums and products: x2+y2−(−2a)x−(−2p)y−b2−q2=0,x^2 + y^2 - (-2a)x - (-2p)y - b^2 - q^2 = 0, which simplifies to x2+y2+2ax+2py−(b2+q2)=0.x^2 + y^2 + 2ax + 2py - (b^2+q^2) = 0.

Answer: Option D

Explanation (Minimal):

  • Use Vieta’s formulas to find sums and products of roots.
  • Substitute into the circle equation with diameter ABAB.
  • The final equation is x2+y2+2ax+2py−(b2+q2)=0x^2+y^2+2ax+2py-(b^2+q^2)=0.