Solveeit Logo
Login

Question

Question: In the following circuit diagram, when $3\Omega$ resistor is removed, then equivalent resistance of ...

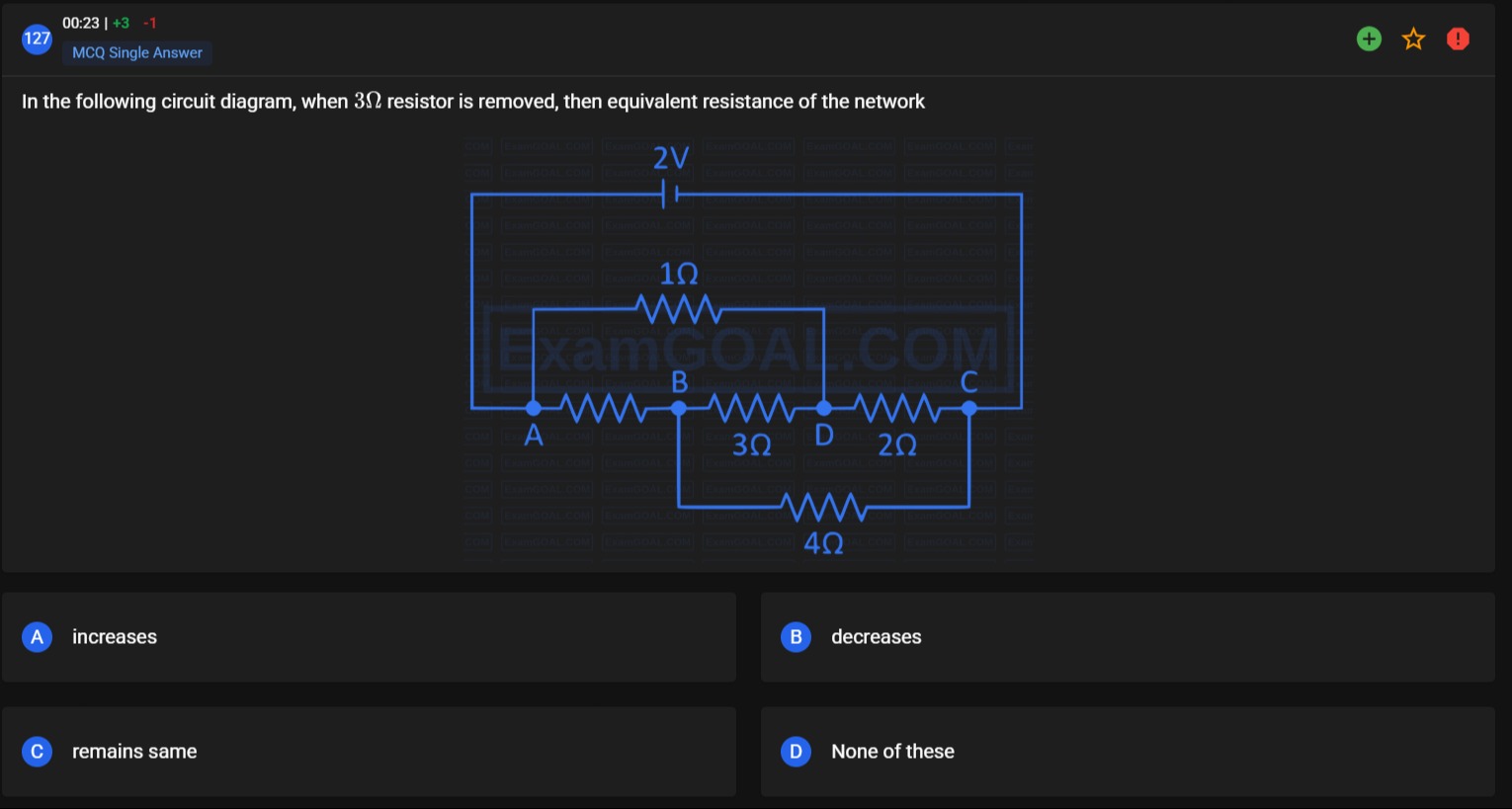
In the following circuit diagram, when 3Ω3\Omega resistor is removed, then equivalent resistance of the network

A

increases

B

decreases

C

remains same

D

None of these

Answer

increases

Explanation

Solution

The equivalent resistance of a network is the total resistance seen by the source connected to it. When a resistor is removed from a network, the current paths available for the flow of charge are altered. Removing a resistor essentially breaks a connection or increases the resistance of a path.

Consider a network of resistors connected between two terminals. If we remove a resistor from this network, we are effectively opening a path for current flow.

  • If the resistor was connected in series with some part of the circuit, removing it will break the circuit if it was the only path. If there are parallel paths, removing one resistor increases the total resistance of that parallel combination.
  • If the resistor was connected in parallel with some part of the circuit, removing it will increase the equivalent resistance of that parallel combination.
  • If the resistor was part of a complex network (like a bridge), removing it will change the current distribution and the equivalent resistance.

In general, adding a resistor between two points in a network provides an additional path for current, which decreases the equivalent resistance between those points (unless the added resistor is in series with the entire network, which is not the case here). Conversely, removing a resistor between two points removes a path for current, which increases the equivalent resistance between those points.

Let ReqR_{eq} be the equivalent resistance of the network with the 3Ω3\Omega resistor present. Let Req′R'_{eq} be the equivalent resistance when the 3Ω3\Omega resistor is removed.

The 3Ω3\Omega resistor is connected between nodes B and D. This resistor provides a path for current flow between B and D. When this resistor is removed, this path is broken.

Removing a resistor from a network generally increases the equivalent resistance of the network as viewed from the terminals, because fewer parallel paths are available for current flow. Adding a resistor generally decreases the equivalent resistance.

Thus, the equivalent resistance of the network increases when the 3Ω3\Omega resistor is removed.