Question

The joint equation of two lines through the origin, each making an angle with measure of 30° with the positive Y -axis, is

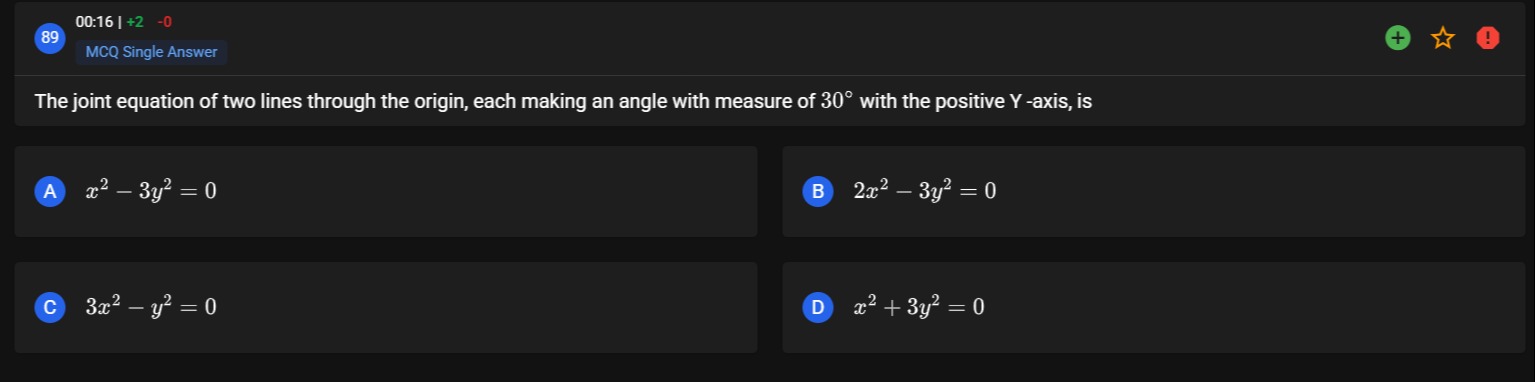
• A. $x^2-3y^2=0$
• B. $2x^2-3y^2=0$
• C. $3x^2-y^2=0$
• D. $x^2+3y^2=0$

Answer 1

Answer: (C)

Option C: $3x^2 - y^2 = 0$

Answer 2

Lines making 30° with the y-axis have inclinations 60° and 120° with the x-axis. Their slopes are $\sqrt{3}$ and $-\sqrt{3}$. The joint equation is $(y - \sqrt{3}x)(y + \sqrt{3}x) = y^2-3x^2=0$, or equivalently, $3x^2 - y^2 = 0$.