Question
Question: 0. $\int sin^4x dx$...
- ∫sin4xdx
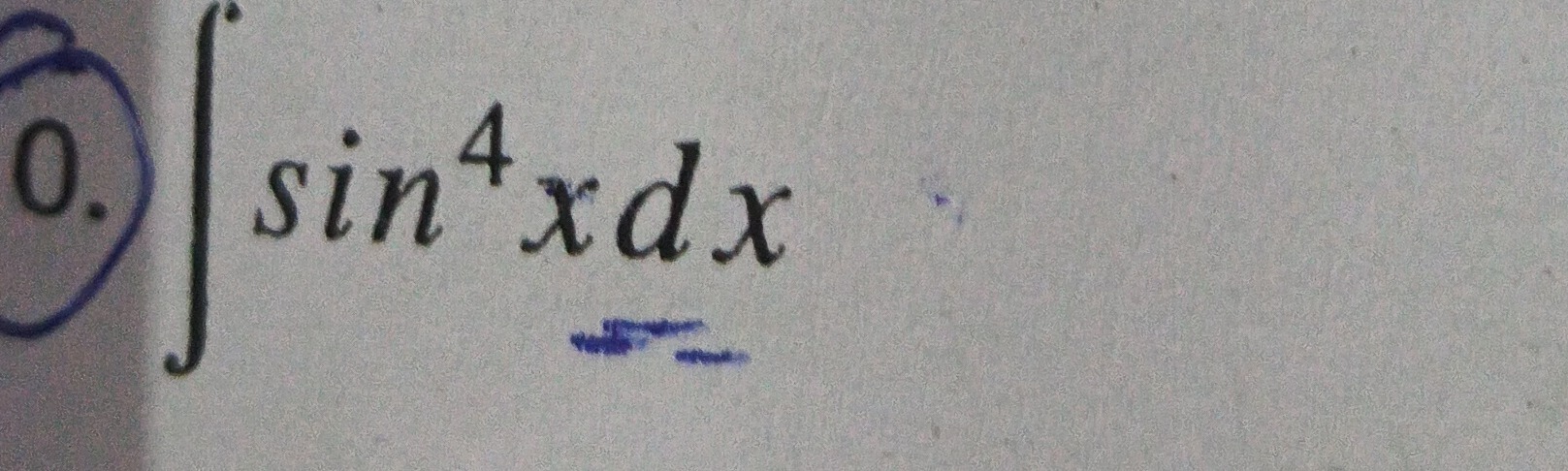
83x−4sin2x+32sin4x+C
Solution
The problem asks to evaluate the integral ∫sin4xdx.
To integrate even powers of sine or cosine, we use power-reducing trigonometric identities. We know the identity: sin2x=21−cos2x
Now, we can express sin4x as (sin2x)2: sin4x=(21−cos2x)2 =41(1−cos2x)2 Expand the squared term: =41(1−2cos2x+cos22x) We have a cos22x term, which is also an even power. We need to reduce its power using another identity: cos2θ=21+cos2θ Here, θ=2x, so: cos22x=21+cos(2⋅2x)=21+cos4x Substitute this back into the expression for sin4x: sin4x=41(1−2cos2x+21+cos4x) To combine the terms inside the parenthesis, find a common denominator: =41(22−24cos2x+21+cos4x) =41(22−4cos2x+1+cos4x) =81(3−4cos2x+cos4x) Now, we can integrate this simplified expression term by term: ∫sin4xdx=∫81(3−4cos2x+cos4x)dx =81∫(3−4cos2x+cos4x)dx Integrate each term:
- ∫3dx=3x
- ∫−4cos2xdx=−4(2sin2x)=−2sin2x
- ∫cos4xdx=4sin4x
Combine these results and add the constant of integration, C: ∫sin4xdx=81(3x−2sin2x+4sin4x)+C Distribute the 81: =83x−82sin2x+32sin4x+C =83x−4sin2x+32sin4x+C
The final answer is 83x−4sin2x+32sin4x+C.
