Question

Vc and VB = VD

Answer 1

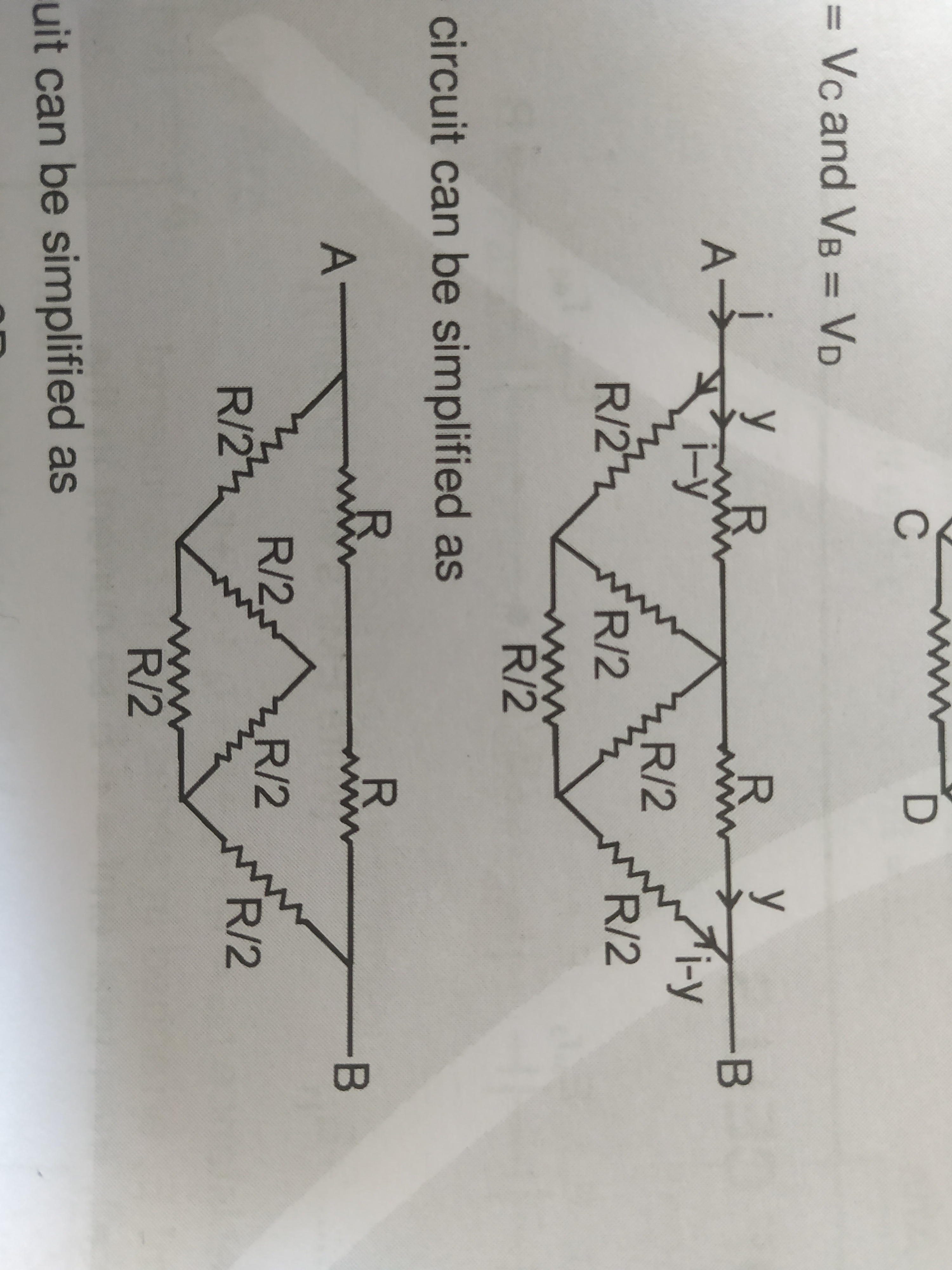
The circuit can be simplified as

Answer 2

The problem statement implies that the second circuit diagram represents a simplification of the first circuit under the condition $V_C = V_D$. This condition indicates a balanced Wheatstone bridge configuration in the section of the circuit between points P and M. The bridge arms are $R_{PC} = R/2$, $R_{PD} = R/2$, $R_{CM} = R$, and $R_{DM} = R$. The balance condition for a Wheatstone bridge is $R_{PC}/R_{PD} = R_{CM}/R_{DM}$. In this case, $(R/2)/(R/2) = 1$ and $R/R = 1$, so the bridge is balanced. When a Wheatstone bridge is balanced, the potential difference between the midpoints (C and D) is zero, meaning $V_C = V_D$. This allows us to simplify the network between P and M. The two paths from P to M are P-C-M and P-D-M. The resistance of path P-C-M is $R_{PC} + R_{CM} = R/2 + R = 3R/2$. The resistance of path P-D-M is $R_{PD} + R_{DM} = R/2 + R = 3R/2$. Since these two paths are in parallel and the bridge is balanced ($V_C = V_D$), they can be treated as parallel resistors. The equivalent resistance between P and M is: $R_{PM} = \frac{R_{P-C-M} \times R_{P-D-M}}{R_{P-C-M} + R_{P-D-M}} = \frac{(3R/2) \times (3R/2)}{(3R/2) + (3R/2)} = \frac{9R^2/4}{3R} = \frac{3R}{4}$ Therefore, the circuit from A to B can be simplified to a series combination of resistors: $R_{AP} = R/2$, $R_{PM} = 3R/4$, and $R_{MB} = R/2$. The total equivalent resistance of the simplified circuit is $R_{AB} = R/2 + 3R/4 + R/2 = R + 3R/4 = 7R/4$. The question asks how the circuit can be simplified, and the second diagram illustrates this simplification by showing the equivalent resistance of the balanced bridge section. The simplification refers to the process of replacing the bridge network with its equivalent resistance, $3R/4$, between points P and M.