Question

Three concentric conducting shells A, B and C have radii r, 2r and 3r and possess charges Q1, Q2 and Q3 respectively. The innermost and the outermost shells are earthed as shown in the figure.

Select the mathematical relations between the charges that are correct:

• A. Q1 + Q3 = -Q2
• B. Q1 = -$\frac{Q2}{4}$
• C. $\frac{Q3}{Q1}$ = 3
• D. $\frac{Q3}{Q2}$ = $\frac{1}{3}$

Answer 1

Answer: (A), (B), (C)

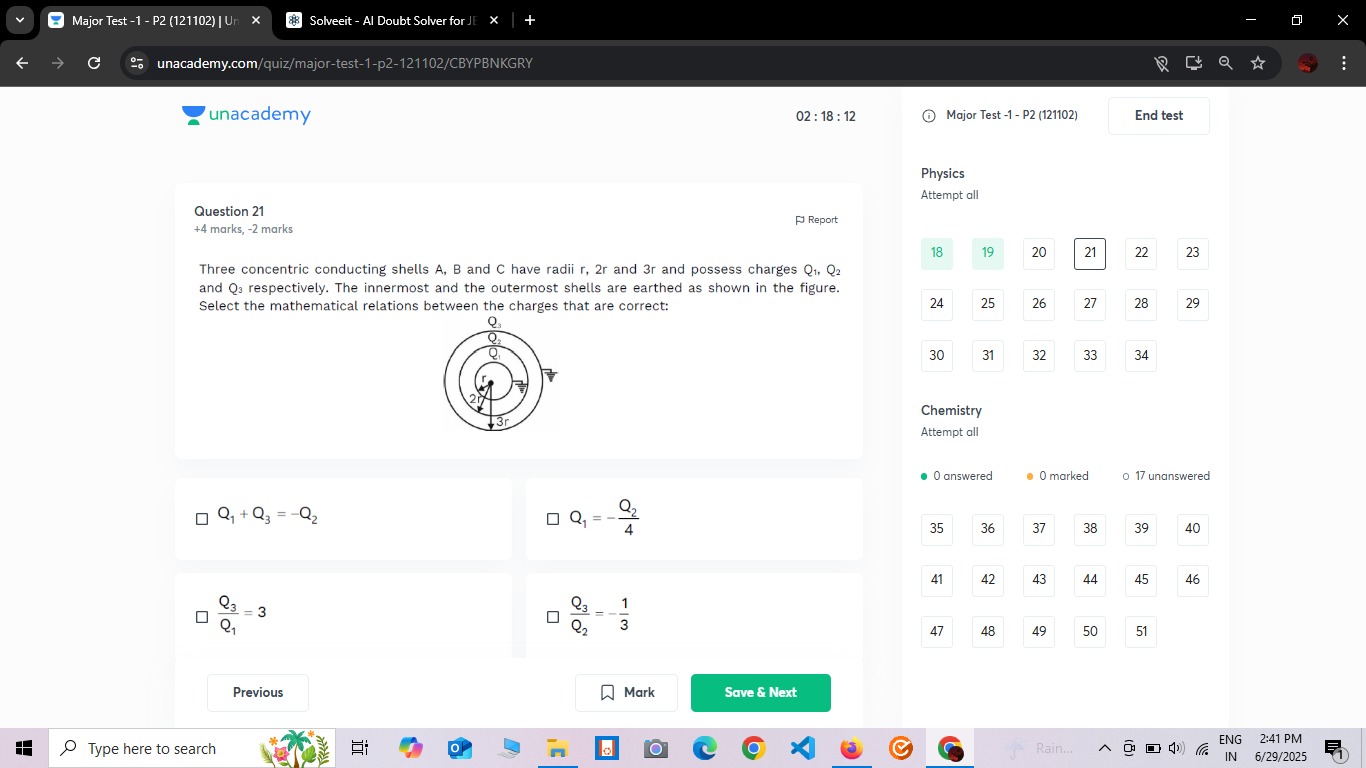
Q1 + Q3 = -Q2, Q1 = -Q2/4, Q3/Q1 = 3

Answer 2

To determine the correct mathematical relations between the charges, we will use the concept of electric potential for concentric conducting shells. When a conductor is earthed, its electric potential becomes zero.

Let $k = \frac{1}{4\pi\epsilon_0}$. The radii of the shells A, B, and C are $r$, $2r$, and $3r$ respectively, and they carry charges $Q_1$, $Q_2$, and $Q_3$.

The potential at the surface of a conducting shell due to its own charge and charges on other concentric shells is given by the superposition principle. For a point on a shell of radius $R$:

• Potential due to charge $Q_i$ on an inner shell of radius $r_i$: $V_i = k \frac{Q_i}{R}$ (since the point is outside the inner shell).
• Potential due to charge $Q_j$ on the same shell of radius $R$: $V_j = k \frac{Q_j}{R}$ (since the point is on the shell).
• Potential due to charge $Q_k$ on an outer shell of radius $r_k$: $V_k = k \frac{Q_k}{r_k}$ (since the point is inside the outer shell, the potential is constant and equal to the potential on the surface of the outer shell).

Given that the innermost shell A (radius $r$) and the outermost shell C (radius $3r$) are earthed, their potentials are zero.

1. Potential of shell A ($V_A = 0$): The potential at the surface of shell A is due to $Q_1$ on A, $Q_2$ on B (outer shell), and $Q_3$ on C (outer shell). $V_A = k \frac{Q_1}{r} + k \frac{Q_2}{2r} + k \frac{Q_3}{3r} = 0$ Multiplying by $\frac{6r}{k}$: $6Q_1 + 3Q_2 + 2Q_3 = 0$ (Equation 1)

2. Potential of shell C ($V_C = 0$): The potential at the surface of shell C is due to $Q_1$ on A (inner shell), $Q_2$ on B (inner shell), and $Q_3$ on C (itself). $V_C = k \frac{Q_1}{3r} + k \frac{Q_2}{3r} + k \frac{Q_3}{3r} = 0$ Multiplying by $\frac{3r}{k}$: $Q_1 + Q_2 + Q_3 = 0$ (Equation 2)

Now we analyze the given options using Equations 1 and 2.

Option 1: $Q_1 + Q_3 = -Q_2$ From Equation 2, $Q_1 + Q_2 + Q_3 = 0$, which directly implies $Q_1 + Q_3 = -Q_2$. This option is correct.

Option 2: $Q_1 = -\frac{Q_2}{4}$ From Equation 2, substitute $Q_3 = -(Q_1 + Q_2)$ into Equation 1: $6Q_1 + 3Q_2 + 2(-(Q_1 + Q_2)) = 0$ $6Q_1 + 3Q_2 - 2Q_1 - 2Q_2 = 0$ $4Q_1 + Q_2 = 0$ $Q_2 = -4Q_1$ This implies $Q_1 = -\frac{Q_2}{4}$. This option is correct.

Option 3: $\frac{Q_3}{Q_1} = 3$ Substitute $Q_2 = -4Q_1$ (from the derivation for Option 2) into Equation 2: $Q_1 + (-4Q_1) + Q_3 = 0$ $-3Q_1 + Q_3 = 0$ $Q_3 = 3Q_1$ This implies $\frac{Q_3}{Q_1} = 3$. This option is correct.

Option 4: $\frac{Q_3}{Q_2} = \frac{1}{3}$ Using the relations $Q_3 = 3Q_1$ and $Q_2 = -4Q_1$: $\frac{Q_3}{Q_2} = \frac{3Q_1}{-4Q_1} = -\frac{3}{4}$ Since $-\frac{3}{4} \neq \frac{1}{3}$, this option is incorrect.

Therefore, the correct mathematical relations are $Q_1 + Q_3 = -Q_2$, $Q_1 = -\frac{Q_2}{4}$, and $\frac{Q_3}{Q_1} = 3.