Question
Question: tan(x+100°) = tanx (tan(x+50°))(tan(x-50°)) Find least positive value of x...
tan(x+100°) = tanx (tan(x+50°))(tan(x-50°))
Find least positive value of x
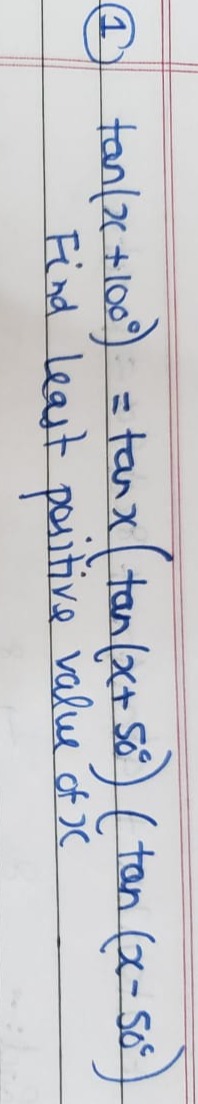
30°
Solution
The given equation is: tan(x+100∘)=tanxtan(x+50∘)tan(x−50∘)
We can rewrite the equation as: tanxtan(x+100∘)=tan(x+50∘)tan(x−50∘)
We use the identity tan(A+B)tan(A−B)=1−tan2Atan2Btan2A−tan2B. Alternatively, and more usefully for this problem, we can use the product-to-sum identity for cosines: tan(A+B)tan(A−B)=cos(A+B)cos(A−B)sin(A+B)sin(A−B) Using sin(X)sin(Y)=21[cos(X−Y)−cos(X+Y)] and cos(X)cos(Y)=21[cos(X−Y)+cos(X+Y)]: tan(A+B)tan(A−B)=cos((A+B)−(A−B))+cos((A+B)+(A−B))cos((A+B)−(A−B))−cos((A+B)+(A−B)) tan(A+B)tan(A−B)=cos(2B)+cos(2A)cos(2B)−cos(2A)
Let A=x and B=50∘. Then A+B=x+50∘ and A−B=x−50∘. So, tan(x+50∘)tan(x−50∘)=cos(2×50∘)+cos(2x)cos(2×50∘)−cos(2x) tan(x+50∘)tan(x−50∘)=cos(100∘)+cos(2x)cos(100∘)−cos(2x)
Substitute this back into the original equation: tan(x+100∘)=tanx(cos(100∘)+cos(2x)cos(100∘)−cos(2x))
Convert tangents to sines and cosines: cos(x+100∘)sin(x+100∘)=cosxsinx(cos(100∘)+cos(2x)cos(100∘)−cos(2x))
Cross-multiply: sin(x+100∘)cosx(cos(100∘)+cos(2x))=cos(x+100∘)sinx(cos(100∘)−cos(2x))
Expand the terms: sin(x+100∘)cosxcos(100∘)+sin(x+100∘)cosxcos(2x)=cos(x+100∘)sinxcos(100∘)−cos(x+100∘)sinxcos(2x)
Rearrange terms to group common factors: cos(100∘)[sin(x+100∘)cosx−cos(x+100∘)sinx]=−cos(2x)[sin(x+100∘)cosx+cos(x+100∘)sinx]
Use the sum/difference formulas for sine: sin(A−B)=sinAcosB−cosAsinB sin(A+B)=sinAcosB+cosAsinB
So, the equation becomes: cos(100∘)sin((x+100∘)−x)=−cos(2x)sin((x+100∘)+x) cos(100∘)sin(100∘)=−cos(2x)sin(2x+100∘)
Use the identity sin(2A)=2sinAcosA: 21sin(2×100∘)=−cos(2x)sin(2x+100∘) 21sin(200∘)=−cos(2x)sin(2x+100∘)
Since sin(200∘)=sin(180∘+20∘)=−sin(20∘): 21(−sin(20∘))=−cos(2x)sin(2x+100∘) 21sin(20∘)=cos(2x)sin(2x+100∘)
Use the product-to-sum identity for sine and cosine: sinAcosB=21[sin(A+B)+sin(A−B)]. Let A=2x+100∘ and B=2x. 21sin(20∘)=21[sin((2x+100∘)+2x)+sin((2x+100∘)−2x)] 21sin(20∘)=21[sin(4x+100∘)+sin(100∘)]
Multiply by 2: sin(20∘)=sin(4x+100∘)+sin(100∘) sin(20∘)−sin(100∘)=sin(4x+100∘)
Use the difference-to-product identity for sine: sinC−sinD=2cos(2C+D)sin(2C−D). 2cos(220∘+100∘)sin(220∘−100∘)=sin(4x+100∘) 2cos(60∘)sin(−40∘)=sin(4x+100∘) 2(21)(−sin(40∘))=sin(4x+100∘) −sin(40∘)=sin(4x+100∘)
Since −sinθ=sin(−θ): sin(−40∘)=sin(4x+100∘)
The general solution for sinθ=sinα is θ=nπ+(−1)nα, where n is an integer. So, 4x+100∘=n×180∘+(−1)n(−40∘).
We need to find the least positive value of x. Case 1: n is an even integer, n=2k. 4x+100∘=2k×180∘+(−1)2k(−40∘) 4x+100∘=360∘k−40∘ 4x=360∘k−140∘ x=90∘k−35∘
For k=0, x=−35∘ (not positive). For k=1, x=90∘−35∘=55∘. (This is a positive value) For k=2, x=180∘−35∘=145∘.
Case 2: n is an odd integer, n=2k+1. 4x+100∘=(2k+1)×180∘+(−1)2k+1(−40∘) 4x+100∘=(2k+1)×180∘+40∘ 4x+100∘=360∘k+180∘+40∘ 4x+100∘=360∘k+220∘ 4x=360∘k+120∘ x=90∘k+30∘
For k=0, x=30∘. (This is a positive value) For k=1, x=90∘+30∘=120∘.
Comparing the positive values obtained: 55∘ and 30∘. The least positive value of x is 30∘.
We must also check for conditions where the tangents are undefined, i.e., when their arguments are (m+1/2)π. x=(m+1/2)π x+50∘=(m+1/2)π x−50∘=(m+1/2)π x+100∘=(m+1/2)π
For x=30∘: tan(30∘) is defined. tan(30∘+50∘)=tan(80∘) is defined. tan(30∘−50∘)=tan(−20∘) is defined. tan(30∘+100∘)=tan(130∘) is defined. None of these angles are odd multiples of 90∘. So x=30∘ is a valid solution.
The final answer is 30°.
